
分析 根据B={x||x|<1},求得B={x|-1<x<1},由A⊆B,及A={x|1<ax<2},解含参数的不等式1<ax<2,对a 进行讨论,并求出此时满足题干的a应满足的条件,解不等式即可求得实数a的范围.
解答 解:∵B={x||x|<1},
∴B={x|-1<x<1},
∵A∪B=B,
∴A⊆B,
∴①A=∅时,a=0,
②a>0时,A={x|$\frac{1}{a}$<x<$\frac{2}{a}$},
∴$\frac{2}{a}$≤1,解得a≥2;
③a<0时,A={x|$\frac{2}{a}$<x<$\frac{1}{a}$},
∴$\frac{2}{a}$≥-1,解得a≤-2;
综上数a的范围为a=0,或a≥2,或a≤-2.
点评 此题是个中档题题.考查集合的包含关系判断及应用,以及绝对值不等式和含参数的不等式的解法,体现了分类讨论的思想,同时也考查学生灵活应用知识分析、解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
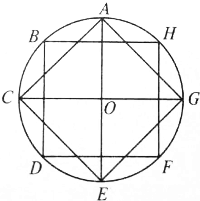 如图所示,A,B,C,D,E,F,G,H是⊙O上的八个等分点,则在以A,B,C,D,E,F,G,H及圆心O这九个点中的任意两点为起点与终点的向量中,模等于半径的向量及模等于半径的$\sqrt{2}$倍的向量分别有( )
如图所示,A,B,C,D,E,F,G,H是⊙O上的八个等分点,则在以A,B,C,D,E,F,G,H及圆心O这九个点中的任意两点为起点与终点的向量中,模等于半径的向量及模等于半径的$\sqrt{2}$倍的向量分别有( )| A. | 8个与8个 | B. | 8个与16个 | C. | 16个与16个 | D. | 16个与8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-3<a<1} | B. | {a|-3≤a≤1} | C. | {a|-2<a<2} | D. | {a|-2≤a≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com