Question

19．已知正六边形ABCDEF，$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{BD}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{DE}$，$\overrightarrow{AD}$．

Answer 1

分析 作出图形，根据相似三角形可得到$\frac{AG}{CG}=\frac{2}{1}$，从而得到$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}$，而同理可得到$\overrightarrow{GD}=\frac{2}{3}\overrightarrow{b}$，这样根据向量加法及减法的几何意义即可表示出$\overrightarrow{AD}，\overrightarrow{DE}$．

解答 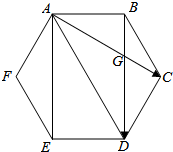解：如图，
设AC交BD于G，则：$\frac{AG}{CG}=\frac{AD}{CB}=\frac{2}{1}$；
∴$AG=\frac{2}{3}AC$；
∴$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}$，同理$\overrightarrow{GD}=\frac{2}{3}\overrightarrow{b}$；
∴$\overrightarrow{AD}=\overrightarrow{AG}+\overrightarrow{GD}=\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$，连接AE，则$\overrightarrow{AE}=\overrightarrow{BD}=\overrightarrow{b}$；
∴$\overrightarrow{DE}$=$\overrightarrow{AE}-\overrightarrow{AD}=\overrightarrow{b}-（\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}）$=$-\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$．

点评 考查正六边形的边及对角线的关系，三角形相似的比例关系，数乘的几何意义，以及向量加法、减法的几何意义．