
【题目】已知数列![]() 是无穷数列,其前n项
是无穷数列,其前n项![]() ,
,![]() ,
,![]() 中的最大项记为
中的最大项记为![]() ,第n项之后的所有项
,第n项之后的所有项![]() ,
,![]() ,
,![]() ,
,![]() 中的最小项记为
中的最小项记为![]() 数列
数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的通项公式
的通项公式![]() ;
;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]()
(3)判断命题“![]() 是常数列的充分不必要条件是
是常数列的充分不必要条件是![]() 为递增的等差数列”的真假,并说明理由.
为递增的等差数列”的真假,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据![]() 通项的二次函数性,可知当
通项的二次函数性,可知当![]() 时,
时,![]() 单调递增且
单调递增且![]() ,从而得到
,从而得到![]() ,整理可得结果;
,整理可得结果;
(2)由![]() 可求得
可求得![]() ,继续代入
,继续代入![]() ,求得
,求得![]() ,以此类推可求得结果;
,以此类推可求得结果;
(3)若![]() 是递增的等差数列,可知
是递增的等差数列,可知![]() ,充分性得证;若
,充分性得证;若![]() 是常数列,存在
是常数列,存在![]() 为常数列的情况,必要性不成立,从而可知原命题为真.
为常数列的情况,必要性不成立,从而可知原命题为真.
(1)由![]() ,可得:
,可得:![]() ,当
,当![]() 时
时![]() 单调递增
单调递增
则![]()
(2)![]() ,
,![]() ,可得:
,可得:![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]()
(3)命题“![]() 是常数列的充分不必要条件是
是常数列的充分不必要条件是![]() 为递增的等差数列”为真命题
为递增的等差数列”为真命题
理由如下:
若![]() 是递增的等差数列,设公差为
是递增的等差数列,设公差为![]()
则![]() ,
,![]()
![]()
即有![]() 是常数列
是常数列 ![]() 充分条件成立
充分条件成立
若![]() 是常数列,可设
是常数列,可设![]() 为常数
为常数![]()
若![]() 可得:
可得:![]() ,即有
,即有![]() 为常数列,是不单调数列
为常数列,是不单调数列 ![]() 必要条件不成立
必要条件不成立
综上可得:![]() 是常数列的充分不必要条件是
是常数列的充分不必要条件是![]() 为递增的等差数列
为递增的等差数列


科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为![]() ,第七个音的频率为
,第七个音的频率为![]() ,则
,则![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的左、右点分别为
的左、右点分别为![]() 点
点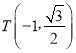 在椭圆上,且
在椭圆上,且![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点(1,0)作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于M、N两点,若
于M、N两点,若![]() 求直线
求直线![]() 的方程;
的方程;
(3)点P、Q为椭圆上的两个动点,![]() 为坐标原点,若直线
为坐标原点,若直线![]() 的斜率之积为
的斜率之积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: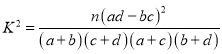 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
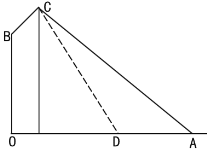
【题目】如图,在路边安装路灯:路宽![]() 米,灯杆长
米,灯杆长![]() 米,且与灯柱
米,且与灯柱![]() 成120°角,路灯采用锥形灯罩,灯罩轴线
成120°角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆垂直且正好通过道路路面的中线.
与灯杆垂直且正好通过道路路面的中线.
(1)求灯柱高![]() 的长度(精确到0.01米);
的长度(精确到0.01米);
(2)若该路灯投射出的光成一个圆锥体,该圆锥体母线与轴线的夹角是30°,写出路灯在路面上投射出的截面图形的边界是什么曲线?写出其相应的几何量(精确到0.01米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com