
| A. | “若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$,则$\overrightarrow a⊥\overrightarrow b$” | |
| B. | 命题“?x∈R,恒有x2+1>0”的否定是“?x0∈R,使得${x_0}^2+1<0$” | |
| C. | ?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 | |
| D. | 设p,q是简单命题,若p∧q是真命题,则(¬p)∨q也是真命题 |
分析 A.利用否命题的定义进行判断.
B.利用全称命题的否定是特称命题进行判断.
C.利用特称命题的性质进行判断.
D.利用复合命题的真假关系进行判断.
解答 解:A.若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$,则$\overrightarrow{a}$与$\overrightarrow{b}$不垂直”,故A错误,
B.命题“?x∈R,恒有x2+1>0”的否定是“?x0∈R,使得x02+1≤0,故B错误,
C.f(x)=x2+mx(x∈R)是奇函数,则f(-x)=-f(x),
即x2-mx=-x2-mx,即x2=-x2,则方程不恒成立,故f(x)不可能是奇函数,故C错误,
D.若p∧q是真命题,则p,q同时为真命题.则(¬p)∨q也是真命题正确,故D正确,
故选:D
点评 本题主要考查命题的真假判断涉及函数的奇偶性,含有量词的命题的否定以及四种命题,复合命题的考查涉及的知识点较多,综合性较强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
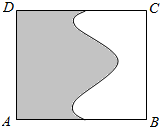 如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.
如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
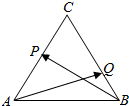 如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.
如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (1,2) | C. | -7 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com