
分析 (1)求出函数的定义域,然后把函数解析式变形,再利用配方法求函数的值域;
(2)令x=2sinα(-$\frac{π}{2}≤α≤\frac{π}{2}$)换元,然后转化为关于α的三角函数求值域.
解答 解:(1)由4x-x2≥0,得0≤x≤4,
∴f(x)=$\frac{\sqrt{4x-{x}^{2}}}{x+2}$=$\sqrt{\frac{4x-{x}^{2}}{(x+2)^{2}}}$=$\sqrt{-\frac{{x}^{2}-4x}{(x+2)^{2}}}$=$\sqrt{-\frac{(x+2)^{2}-8(x+2)+12}{(x+2)^{2}}}$=$\sqrt{-12\frac{1}{(x+2)^{2}}+8\frac{1}{x+2}-1}$,
∵0≤x≤4,
∴$\frac{1}{6}≤\frac{1}{x+2}≤\frac{1}{2}$,
∴当$\frac{1}{x+2}=\frac{1}{3}$时,$f(x)_{max}=\sqrt{-12×\frac{1}{9}+8×\frac{1}{3}-1}$=$\frac{\sqrt{3}}{3}$,
当$\frac{1}{x+2}=\frac{1}{6}=\frac{1}{2}$时,$f(x)_{min}=\sqrt{-12×\frac{1}{4}+8×\frac{1}{2}-1}$=0.
∴函数f(x)=$\frac{\sqrt{4x-{x}^{2}}}{x+2}$的值域为[0,$\frac{\sqrt{3}}{3}$];
(2)令x=2sinα(-$\frac{π}{2}≤α≤\frac{π}{2}$),则x2=4sin2α,
∴y=x+$\sqrt{4-{x}^{2}}$=2sinα$+\sqrt{4-4si{n}^{2}α}$=2sinα+2cosα=$2\sqrt{2}sin(α+\frac{π}{4})$,
∵$-\frac{π}{2}≤α≤\frac{π}{2}$,
∴$-\frac{π}{4}≤α+\frac{π}{4}≤\frac{3π}{4}$.
则$-\frac{\sqrt{2}}{2}≤sin(α+\frac{π}{4})≤1$,
则-2$≤y≤2\sqrt{2}$.
∴y=x+$\sqrt{4-{x}^{2}}$的值域为[-2,$2\sqrt{2}$].
点评 本题考查函数值域的求法,考查了配方法及换元法求函数的值域,是中档题.


科目:高中数学 来源: 题型:填空题
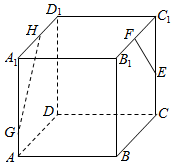 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
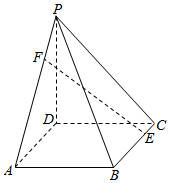 如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{12}{5}$ | C. | -2 | D. | -$\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com