
| A. | a+b>0 | B. | a+b>1 | C. | 2a+b>0 | D. | 2a+b>1 |
分析 结合对数函数与绝对值可得-ln(a+1)=ln(b+1),从而可得ab+a+b=0;从而由基本不等式可得(a+b)(a+b+4)>0,从而判断.
解答 解:易知y=ln(x+1)在定义域上是增函数,
而f(x)=|ln(x+1)|,且f(a)=f(b);
故-ln(a+1)=ln(b+1),
即ab+a+b=0.
$0=ab+a+b<\frac{{{{({a+b})}^2}}}{4}+a+b$,
即(a+b)(a+b+4)>0,
显然-1<a<0,b>0,
∴a+b+4>0,
∴a+b>0,
故选A.
点评 本题考查了对数函数与绝对值函数的性质的判断与应用,同时考查了基本不等式与转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
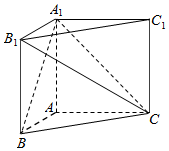 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
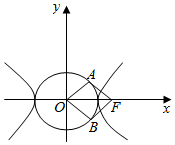 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
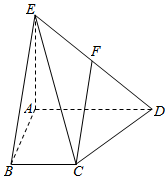 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
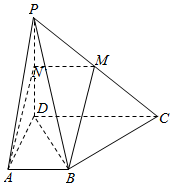 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com