
分析 先求出x1的范围,再将x1f(x2)转化为x的函数,利用导数知识确定x1f(x2)的取值范围.
解答 解:∵4≤x2≤6时,f(x)=log2(x-2)∈[1,2]
∴由-x2+4x∈[1,2]得2-$\sqrt{3}$≤x1≤2-$\sqrt{2}$或2+$\sqrt{2}$≤x1≤2+$\sqrt{3}$.
∵f(x1)=-x12+4x1,f(x1)=f(x2)
∴x1f(x2)=x1f(x1)=x1(-x12+4x1)
令y=x1f(x2)=x1(-x12+4x1)
则y′=x1(-3x1+8)
∴2-$\sqrt{3}$≤x1≤2-$\sqrt{2}$或2+$\sqrt{2}$≤x1≤$\frac{8}{3}$时,函数单调递增;$\frac{8}{3}$≤x1≤2+$\sqrt{3}$时,函数单调递减
∴x1f(x2)的取值范围为[3,$\frac{256}{27}$].
故答案为[3,$\frac{256}{27}$].
点评 本题考查分段函数,考查导数知识的运用,正确转化是解题的关键所在.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
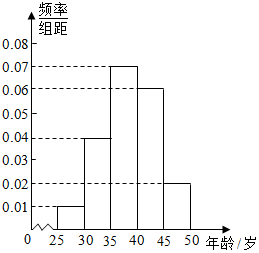 某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:| 分组(岁) | 频数 |
| [25,30) | 5 |
| [30,35) | x |
| [35,40) | 35 |
| [40,45) | y |
| [45,50] | 10 |
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值2 | B. | 最大值2 | C. | 最小值1 | D. | 最大值1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥3 | B. | a≤3 | C. | a<3 | D. | a>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com