
分析 (I)由题意可得:2c=2,$\frac{4}{9{a}^{2}}+\frac{24}{9{b}^{2}}$=1,又a2=b2+c2,联立解出即可得出.
(II)由题意可设直线l的方程为:x=my+4,代入椭圆方程可得:(3m2+4)y2+2my+36=0,由△>0,解得m2>4.设A(x1,y1),B(x2,y2).令λ=$\frac{{S}_{△AOD}}{{S}_{△BOD}}$=$\frac{\frac{1}{2}|OD||{y}_{1}|}{\frac{1}{2}|OD||{y}_{2}|}$=$\frac{{y}_{1}}{{y}_{2}}$,λ∈(0,1).把y1=λy2代入根与系数的关系,解得:m2=$\frac{4(λ+1)^{2}}{10λ-3{λ}^{2}-3}$>4,解出即可得出.
解答 解:(I)∵椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的焦距为2,且经过点(${\frac{2}{3}$,$\frac{{2\sqrt{6}}}{3}}$),
∴2c=2,$\frac{4}{9{a}^{2}}+\frac{24}{9{b}^{2}}$=1,又a2=b2+c2,联立解得a=2,c=1,b2=3.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(II)由题意可设直线l的方程为:x=my+4,代入椭圆方程可得:(3m2+4)y2+24my+36=0,由△>0,解得m2>4.
设A(x1,y1),B(x2,y2).∴y1+y2=$\frac{-24m}{3{m}^{2}+4}$,y1y2=$\frac{36}{3{m}^{2}+4}$,(*),
令λ=$\frac{{S}_{△AOD}}{{S}_{△BOD}}$=$\frac{\frac{1}{2}|OD||{y}_{1}|}{\frac{1}{2}|OD||{y}_{2}|}$=$\frac{{y}_{1}}{{y}_{2}}$,λ∈(0,1).
把y1=λy2代入(*)可得:$\frac{(λ+1)^{2}}{λ}$=$\frac{16{m}^{2}}{3{m}^{2}+4}$,解得:m2=$\frac{4(λ+1)^{2}}{10λ-3{λ}^{2}-3}$>4,
则λ≠1,且3λ2-10λ+3<0,解得$\frac{1}{3}<λ<1$,
∴△AOD与△BOD面积之比的取值范围是$(\frac{1}{3},1)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、三角形面积计算公式、不等式的解法,考查了推理能力与计算能力,属于难题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
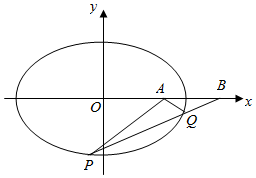 已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.
已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
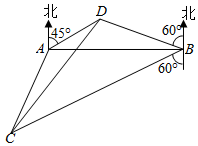 2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?
2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 160 | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | ¬p∨q | C. | ¬p∧q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com