某电视台推出一档游戏类综艺节目.选手面对1-5号五扇大门.依次按响门上的门铃.门铃会播放一段音乐.选手需正确回答这首歌的名字.回答正确.大门打开.并获得相应的家庭梦想基金.回答每一扇门后.选手可自由选择带着目前奖金离开.还是继续挑战后面的门以获得更多的梦想基金.但是一旦回答错误.游戏结束并将之前获得的所有梦想基金清零,整个游戏过程中.选手有一次求助机会.选手可以询问亲友团成员以� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

15．某电视台推出一档游戏类综艺节目，选手面对1-5号五扇大门，依次按响门上的门铃，门铃会播放一段音乐，选手需正确回答这首歌的名字，回答正确，大门打开，并获得相应的家庭梦想基金，回答每一扇门后，选手可自由选择带着目前奖金离开，还是继续挑战后面的门以获得更多的梦想基金，但是一旦回答错误，游戏结束并将之前获得的所有梦想基金清零；整个游戏过程中，选手有一次求助机会，选手可以询问亲友团成员以获得正确答案．
1-5号门对应的家庭梦想基金依次为3000元，6000元，8000元、12000元、24000元（以上基金金额为打开大门后的累积金额）设某选手正确回答每扇门的歌曲名字的概率均为Pi且P_i=$\frac{6-i}{7-i}$（i=1，2，…，5），亲友团正确回答每一扇门的歌曲名字的概率均为$\frac{1}{5}$，该选手正确回答每一扇门的歌名后选择继续挑战后面的门的概率均为$\frac{1}{2}$；
（1）求选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率；
（2）若选手在整个游戏过程中不使用求助，且获得的家庭梦想基金数额为X元，求X的分布列和数学期望．

分析（1）记事件“选手正确回答第i扇门歌曲”为Ai记事件“亲友团正确回答歌曲名字”为B，记事件“回答正确后选择继续挑战”为C，第三扇门选手答不出才求助，由此能求出选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率．
（2）X可能的取值有：0，3000，6000，8000，12000，24000，分别求出相应的概率，由此能求出X的分布列和数学期望．

解答解：（1）记事件“选手正确回答第i扇门歌曲”为Ai
记事件“亲友团正确回答歌曲名字”为B，
记事件“回答正确后选择继续挑战”为C，
则对应事件的概率分别为$P（{A_1}）=\frac{5}{6}，P（{A_2}）=\frac{4}{5}，P（{A_3}）=\frac{3}{4}，P（{A_4}）=\frac{2}{3}，P（{A_5}）=\frac{1}{2}$，
$P（B）=\frac{1}{5}，P（C）=\frac{1}{2}$
因此题目所求概率为P（A₁）P（A₂）P（$\overline{{A}_{3}}$）P（A₄）P（B）P⁴（C）=$\frac{5}{6}×\frac{4}{5}×\frac{1}{4}×\frac{2}{3}×\frac{1}{5}×\frac{1}{{2}^{4}}$=$\frac{1}{720}$．
注意：第三扇门选手答不出才求助
（2）X可能的取值有：0，3000，6000，8000，12000，24000，
$P（X=3000）=\frac{5}{6}\frac{1}{2}=\frac{5}{12}$，
$P（X=6000）=\frac{5}{6}\frac{4}{5}\frac{1}{2^2}=\frac{1}{6}$，
$P（X=8000）=\frac{5}{6}\frac{4}{5}\frac{3}{4}\frac{1}{2^3}=\frac{1}{16}$，
$P（X=12000）=\frac{5}{6}\frac{4}{5}\frac{3}{4}\frac{2}{3}\frac{1}{2^4}=\frac{1}{48}$，
$P（X=24000）=\frac{5}{6}\frac{4}{5}\frac{3}{4}\frac{2}{3}\frac{1}{2}\frac{1}{2^4}=\frac{1}{96}$，
$P（X=0）=1-P（3000）-P（6000）-P（8000）-P（12000）-P（24000）=\frac{31}{96}$，
∴X的分布列为

X	0	3000	6000	8000	12000	24000
P	$\frac{31}{96}$	$\frac{5}{12}$	$\frac{1}{6}$	$\frac{1}{16}$	$\frac{1}{48}$	$\frac{1}{96}$

∴EX=0×$\frac{31}{96}$+3000×$\frac{5}{12}$+6000×$\frac{1}{6}$+8000×$\frac{1}{16}$+12000×$\frac{1}{48}$+24000×$\frac{1}{96}$=3250．
注意：最后一次答对无需再选择．

点评本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意对立事件概率计算公式的合理运用．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

5．

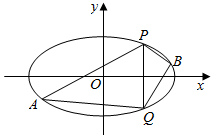已知椭圆C的中心在原点，焦点在x轴上，离心率为$\frac{\sqrt{3}}{2}$，它的一个顶点恰好是抛物线x²=4$\sqrt{2}$y的焦点．
（1）求椭圆C的方程；
（2）直线x=2与椭圆交于P，Q两点，P点位于第一象限，A，B是椭圆上位于直线x=2两侧的动点．当点A，B运动时，满足∠APQ=∠BPQ，问直线AB的斜率是否为定值，如果为定值，求出斜率的值；如果不为定值，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁，F₂，且|F₁F₂|=2，点P（2，$\frac{2\sqrt{5}}{5}$）在椭圆上．
（1）求椭圆C的方程；
（2）设O为坐标原点，圆O：x²+y²=a²，B₁（0，-b），B₂（0，b），E为椭圆C上异于顶点的任意一点，点F在圆O上，且EF⊥x轴，E与F在x轴两侧，直线EB₁，EB₂分别与x轴交于点C，H，记直线FG，FH的斜率分别为k₁，k₂，问：k₁k₂是否为定值？若是，求出该定值；若不是，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．已知实数x，y满足$\frac{{x}^{2}}{3}$+y²=1，则u=|3x+3y-7|的取值范围为[1，13]．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁，F₂，点P在椭圆上，如果PF₁的中点在y轴上，且|PF₁|=$\frac{5}{3}$|PF₂|，则椭圆的离心率e为$\frac{1}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的焦距为2．且经过点（${\frac{2}{3}$，$\frac{{2\sqrt{6}}}{3}}$）．
（I）求椭圆C的方程；
（Ⅱ）若过点D（4，O）的直线l与C交于不同的两点A，B，且A在DB之间，试求△AOD与△BOD面积之比的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知等差数列{a_n}的首项a₁=1，公差d＞0，且a₂，a₅，a₁₄分别等于等比数列{b_n}的b₂，b₃，b₄．
（1）求数列{a_n}与{b_n}的通项公式；
（2）设数列{c_n}满足c_n=$\left\{\begin{array}{l}{3（n=1）}\\{{a}_{n}+2{b}_{n}（n≥2）}\end{array}\right.$，求c₁+c₂+…+c₁₀₀的值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

4．已知实数x，y满足$\left\{\begin{array}{l}{x≥1}\\{x-2y+5≥0}\\{x-y≤0}\end{array}\right.$且z=4x-y的最大值是最小值的m倍，则m=15．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

5．已知数列{a_n}是公比大于1的等比数列，且a₃+a₅=20，a₄=8，则其前n项和S_n=2ⁿ-1．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学