
分析 令t=3x+3y-7,与椭圆方程联立,由判别式等于0求得t的范围,则u=|3x+3y-7|的取值范围可求.
解答 解:令t=3x+3y-7,即$y=-x+\frac{t}{3}+\frac{7}{3}$,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{3}+{y}^{2}=1}\\{y=-x+\frac{t}{3}+\frac{7}{3}}\end{array}\right.$,得12x2-6(t+7)x+t2+14t+40=0.
由△=36(t+7)2-48(t2+14t+40)=0,
得t2-14t+13=0,即t=1或t=13.
∴u=|3x+3y-7|的取值范围为[1,13].
故答案为:[1,13].
点评 本题考查椭圆的简单性质,考查了直线和椭圆位置关系的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
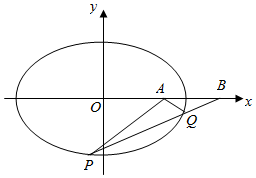 已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.
已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
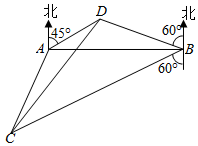 2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?
2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 160 | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x0+1≤0,则¬p:?x∈R,x+1>0 | |
| C. | △ABC中,sinA>sinB是A>B的充要条件 | |
| D. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$<0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com