
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x0+1≤0,则¬p:?x∈R,x+1>0 | |
| C. | △ABC中,sinA>sinB是A>B的充要条件 | |
| D. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$<0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角 |
分析 A.根据逆否命题的定义进行判断,
B.根据含有量词的命题的否定进行判断,
C.根据正弦定理以及充分条件和必要条件的定义进行判断,
D.根据向量数量积以及夹角关系进行判断.
解答 解:A.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”,正确为真命题,
B.若命题p:?x0∈R,x0+1≤0,则¬p:?x∈R,x+1>0,命题为真命题,
C.△ABC中,sinA>sinB等价为a>b,等价为A>B,则△ABC中,sinA>sinB是A>B的充要条件为真命题.
D.当向量$\overrightarrow{a}$,$\overrightarrow{b}$反向共线时,夹角为180°,满足$\overrightarrow{a}$•$\overrightarrow{b}$<0,但$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角错误,故D错误,
故选:D
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件的判断,四种命题的关系以及含有量词的命题的否定,涉及的知识点较多,综合性较强,但难度不大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
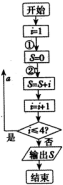 执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )
执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
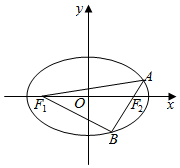 已知中心在原点O的椭圆左,右焦点分别为F1,F2,F2(1,0),且椭圆过点(1,$\frac{3}{2}$).
已知中心在原点O的椭圆左,右焦点分别为F1,F2,F2(1,0),且椭圆过点(1,$\frac{3}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n-1 | B. | n | C. | 2n | D. | n2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com