练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．${∫}_{0}^{2π}$|cosx|dx=4．

    分析 根据定积分的计算法则计算即可．

    解答 解：${∫}_{0}^{2π}$|cosx|dx=${∫}_{0}^{\frac{π}{2}}$cosxdx+${∫}_{\frac{3π}{2}}^{2π}$cosxdx-${∫}_{\frac{π}{2}}^{\frac{3π}{2}}$cosdx=sinx|${\;}_{0}^{\frac{π}{2}}$+sinx|${\;}_{\frac{3π}{2}}^{2π}$-sinx|${\;}_{\frac{π}{2}}^{\frac{3π}{2}}$=1+1-（-1-1）=4，
    故答案为：4．

    点评 本题考查了分段函数的定积分的计算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．下列命题错误的是（　　）
    A．命题“若x2+y2=0，则x=y=0”的逆否命题为“若x，y中至少有一个不为0，则x2+y2≠0”
    B．若命题p：?x0∈R，x0+1≤0，则￢p：?x∈R，x+1＞0
    C．△ABC中，sinA＞sinB是A＞B的充要条件
    D．若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$＜0，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知△ABC的边AB长为4，若BC边上的中线为定长3，求顶点C的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．为推广漳州“三宝”，某商场推出“砸金蛋”促销活动，单笔购满50元可以玩一次“砸金蛋”游戏，每次游戏可以砸两个金蛋，每砸一个金蛋可以等可能地得到“水仙花卡片”，“片仔癀卡片”和“八宝印泥卡片”中的一张，如果一次游戏中可以得到相同的卡片，那么该商场赠送一份奖品，则玩一次该游戏可以获赠一份奖品的概率是$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．一客户到某家政服务公司随机选聘2名服务员，现该公司共有5名服务员可供选聘，其中A类服务员2名（记为A1、A2），B类服务员3名（记为B1、B2、B3）．
    （1）写出所有的基本事件；
    （2）求客户只选聘B类服务员的概率；
    （3）求客户至少选聘1名B类服务员的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若甲乙两人从A，B，C，D，E，F六门课程中选修三门，若甲不选修A，乙不选修F，则甲乙两人所选修课程中恰有两门相同的选法有（　　）
    A．42种B．72种C．84种D．144种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

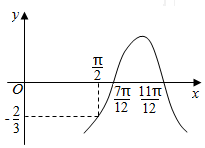
    15．已知函数f（x）=Acos（ωx+φ）（ω＞0）的部分图象如图所示，下面结论错误的是（　　）
    A．函数f（x）的最小周期为$\frac{2π}{3}$
    B．图象f（x）的图象可由g（x）=Acos（ωx）的图象向右平移$\frac{π}{12}$个单位得到
    C．函数f（x）的图象关于直线x=$\frac{π}{12}$对称
    D．函数f（x）在区间（$\frac{π}{4}$，$\frac{π}{2}$）上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若椭圆的方程$\frac{x^2}{10-a}+\frac{y^2}{a-2}$=1，且此椭圆的离心率为$\frac{{\sqrt{2}}}{2}$，则实数a=$\frac{14}{3}$或$\frac{22}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知sinα=$\frac{5}{13}$，且$\frac{π}{2}$＜α＜π，则tan2α=$-\frac{120}{119}$．．

    查看答案和解析>>

    同步练习册答案