
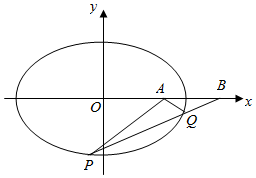
 已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.
已知椭圆:$\frac{{x}^{2}}{2}$+y2=1,已知A(1,0).B(2,0),若过B的直线与椭圆C交于P、Q两点.分析 (1)设过B的直线方程为y=k(x-2),代入椭圆方程x2+2y2-2=0,运用韦达定理和判别式大于0,求得直线PA和QA的斜率之和,化简整理可得0,即可得证;
(2)△QPA面积S=S△PAB-S△QAB=$\frac{1}{2}$|AB|•|y1-y2|,由P,Q满足直线方程,再由韦达定理,化简整理,运用换元法和配方,由二次函数的最值求法,即可得到所求最大值.
解答 解:(1)证明:设过B的直线方程为y=k(x-2),
代入椭圆方程x2+2y2-2=0,可得
(1+2k2)x2-8k2x+8k2-2=0,
设P(x1,y1),Q(x2,y2),
△=64k4-4(1+2k2)(8k2-2)>0,可得-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$,
x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-2}{1+2{k}^{2}}$,
直线PA和QA的斜率之和为$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$
=$\frac{k({x}_{1}-2)}{{x}_{1}-1}$+$\frac{k({x}_{2}-2)}{{x}_{2}-1}$=k•$\frac{2{x}_{1}{x}_{2}-3({x}_{1}+{x}_{2})+4}{({x}_{1}-1)({x}_{2}-1)}$
由2x1x2-3(x1+x2)+4=$\frac{16{k}^{2}-4}{1+2{k}^{2}}$-$\frac{24{k}^{2}}{1+2{k}^{2}}$+4=$\frac{-4-8{k}^{2}}{1+2{k}^{2}}$+4=-4+4=0,
可得直线PA和QA的斜率之和为0,
即有tan∠QAB=-tan∠PAB,
则∠QAB+∠PAB=π;
(2)△QPA面积S=S△PAB-S△QAB=$\frac{1}{2}$|AB|•|y1-y2|
=$\frac{1}{2}$|k|•|x1-x2|=$\frac{1}{2}$|k|•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{1}{2}$|k|•$\sqrt{\frac{64{k}^{4}}{(1+2{k}^{2})^{2}}-\frac{4(8{k}^{2}-2)}{1+2{k}^{2}}}$=$\frac{\sqrt{2{k}^{2}-4{k}^{4}}}{1+2{k}^{2}}$,
令t=1+2k2,即有2k2=t-1,
则S=$\frac{\sqrt{t-1-(t-1)^{2}}}{t}$=$\sqrt{-\frac{2}{{t}^{2}}+\frac{3}{t}-1}$=$\sqrt{-2(\frac{1}{t}-\frac{3}{4})^{2}+\frac{1}{8}}$,
当$\frac{1}{t}$=$\frac{3}{4}$,即t=$\frac{4}{3}$,可得k=±$\frac{\sqrt{6}}{6}$∈(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
面积S取得最大值$\frac{\sqrt{2}}{4}$.
点评 本题考查直线方程和椭圆方程联立,运用韦达定理和判别式大于0,考查直线的斜率的运用,同时考查三角形的面积的最值的求法,注意运用面积相减法,考查换元法和二次函数的最值的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
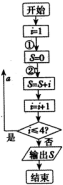 执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )
执行如图所示的程序框图.设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出S的值为n,则m+n=( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com