
分析 (Ⅰ)求出函数的导数,得到关于a的方程,解出即可;(Ⅱ)问题转化为f(x)不存在最小值,通过讨论a的范围求出函数的单调性,判断函数有无最小值,从而确定a的范围即可.
解答 (Ⅰ)解:函数y=f(x)的定义域D={x|x∈R且x≠-a},
由题意,f′(a)有意义,所以a≠0.
求导,得f′(x)=-$\frac{(x+a)(x-3a)}{{(x+a)}^{4}}$.…(3分)
所以f′(a)=$\frac{1}{{4a}^{2}}$=1,解得:a=±$\frac{1}{2}$.…(5分)
(Ⅱ)解:“对于定义域内的任意x1,总存在x2使得f(x2)<f(x1),
等价于“f(x)不存在最小值”. …(6分)
①当a=0时,
由f(x)=$\frac{1}{x}$,得f(x)无最小值,符合题意. …(8分)
②当a<0时,
令f′(x)=0,得x=-a 或x=3a.…(9分)
随着x的变化时,f′(x)与f(x)的变化情况如下表:
| x | (-∞,3a) | 3a | (3a,-a) | -a | (-a,+∞) |
| f′(x) | - | 0 | + | 不存在 | - |
| f(x) | ↘ | 极小 | ↗ | 不存在 | ↘ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{7}{9}$ | C. | $\frac{15}{16}$ | D. | $\frac{17}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
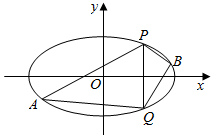 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com