
分析 (1)建立平面直角坐标系,由已知令$\overrightarrow a=(4,0)$,$\overrightarrow b=(0,2)$,$\overrightarrow c=(x,y)$,求得$\overrightarrow{a}-2\overrightarrow{b}$的坐标,代入向量模的公式计算;
(2)由$(\overrightarrow c-\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,得(x-2)2+(y-1)2=5,令$x=2+\sqrt{5}cosθ$,$y=1+\sqrt{5}sinθ$,求出$|\overrightarrow{c}|$,利用辅助角公式化积后得答案.
解答 解:(1)建立平面直角坐标系,令$\overrightarrow a=(4,0)$,$\overrightarrow b=(0,2)$,$\overrightarrow c=(x,y)$,
则$\overrightarrow a-2\overrightarrow b=(4,0)-2(0,2)=(4,-4)$,
∴$|\overrightarrow a-2\overrightarrow b|=\sqrt{{4^2}+{{(-4)}^2}}=4\sqrt{2}$;
(2)∵$(\overrightarrow c-\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=(x-4,y)•(x,y-2)=0$,
∴(x-2)2+(y-1)2=5,
令$x=2+\sqrt{5}cosθ$,$y=1+\sqrt{5}sinθ$,
则$|\overrightarrow c|=\sqrt{{x^2}+{y^2}}=\sqrt{{{(2+\sqrt{5}cosθ)}^2}+{{(1+\sqrt{5}sinθ)}^2}}$
=$\sqrt{10+4\sqrt{5}cosθ+2\sqrt{5}sinθ}$=$\sqrt{10+10sin(θ+φ)}≤\sqrt{10+10}=2\sqrt{5}$.
故$|\overrightarrow c|$的最大值为$2\sqrt{5}$.
点评 本题考查平面向量的数量积运算,考查了向量加减法的坐标运算,训练了向量模的求法,是中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,-\frac{1}{8})$ | B. | $(-\frac{1}{8},0)$ | C. | $(0,-\frac{1}{2})$ | D. | $(-\frac{1}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
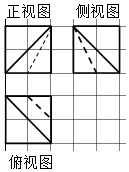 如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )
如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{19}{3}$ | C. | 6 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com