
分析 (Ⅰ)根据导数的几何意义即可求出切线方程,
(Ⅱ)先求出函数的导数,通过讨论a的范围,得到函数的单调区间,
(Ⅲ)要证:f′(u)<k.,只需证$\frac{λ}{{{x_2}+(λ-1)x{\;}_1}}-\frac{{ln{x_2}-ln{x_1}}}{{x{\;}_2-{x_1}}}<0$,构造函数令$g(t)=\frac{λ(t-1)}{t+λ-1}-lnt$,通过讨论函数的单调性,从而证出结论.
解答 解:(Ⅰ)当a=1时,f(x)=lnx+x2+x,
∴$f'(x)=\frac{1}{x}+2x+1$,
∴f'(1)=4
又∵f(1)=ln1+12+1=2,
∴函数f(x)的图象在点(1,f(1))处的切线方程为:y-2=4(x-1),
即4x-y-2=0.
(Ⅱ)f(x)的定义域为(0,+∞)$f'(x)=\frac{1}{x}+2ax+1=\frac{{2a{x^2}+x+1}}{x}$,
当a≥0时,f'(x)>0在(0,+∞)上恒成立,f(x)在定义域内单调递增;
当a<0时,令f'(x)=0,解得,$x=\frac{{-1±\sqrt{1-8a}}}{4a}$,
∵x>0,
∴$x=\frac{{-1-\sqrt{1-8a}}}{4a}$
则$x∈(0,\frac{{-1-\sqrt{1-8a}}}{4a})$时,f'(x)>0,f(x)单调递增;
$x∈(\frac{{-1-\sqrt{1-8a}}}{4a},+∞)$时,f'(x)<0,f(x)单调递减;
综上,a≥0时,f(x)的单调递增区间为(0,+∞);
a<0时,f(x)的单调递增区间为$(0,\frac{{-1-\sqrt{1-8a}}}{4a})$,f(x)的单调递增区间为$(\frac{{-1-\sqrt{1-8a}}}{4a},+∞)$
(Ⅲ)证明:$k=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{ln{x_2}+a{x_2}^2+{x_2}-ln{x_1}-a{x_1}^2-{x_1}^{\;}}}{{{x_2}-{x_1}}}$=$\frac{{ln{x_2}-ln{x_1}}}{{x{\;}_2-{x_1}}}+a({x_1}+{x_2})+1$,
∵$N(u,0),A({x_1},{y_2}),B({x_2},{y_2}),\overrightarrow{AB}=λ\overrightarrow{AN}(1≤λ≤2)$,
∴x2-x1=λ(u-x1),
∴$u=\frac{{{x_2}+(λ-1){x_1}}}{λ}$,
又$f'(x)=\frac{1}{x}+2ax+1$,
∴$f'(u)=\frac{λ}{{{x_2}+(λ-1)x{\;}_1}}+2a\frac{{{x_2}+(λ-1){x_1}}}{λ}+1$,
∴$f'(u)-k=\frac{λ}{{{x_2}+(λ-1)x{\;}_1}}-\frac{{ln{x_2}-ln{x_1}}}{{x{\;}_2-{x_1}}}+\frac{a}{λ}(2-λ)({x_2}-{x_1})$,
∵a<0,x2>x1,1≤λ≤2,
∴$\frac{a}{λ}(2-λ)({x_2}-{x_1})<0$
要证:f′(u)<k.,只需证$\frac{λ}{{{x_2}+(λ-1)x{\;}_1}}-\frac{{ln{x_2}-ln{x_1}}}{{x{\;}_2-{x_1}}}<0$
即证:$\frac{{λ({x_2}-{x_1})}}{{{x_2}+(λ-1)x{\;}_1}}-(lnx_2^{\;}-ln{x_1})<0$,设$t=\frac{x_2}{x_1}>1$
令$g(t)=\frac{λ(t-1)}{t+λ-1}-lnt$,
则$g'(t)=\frac{{-{t^2}+({λ^2}-2λ+2)t-{{(λ-1)}^2}}}{{{{(t+λ-1)}^2}t}}$,
令h(t)=-t2+(λ2-2λ+2)t-(λ-1)2,t>1,1≤λ≤2
对称轴$t=\frac{{{{(λ-1)}^2}+1}}{2}≤1$.h(t)<h(1)=0,
∴g'(t)<0,
故g(t)在(1,+∞)内单调递减,则g(t)<g(1)=0,
故f′(u)<k.
点评 本题考查导数知识的运用,考查函数的单调性,考查分离参数法的运用,考查不等式的证明,构造函数,正确求导是关键.


科目:高中数学 来源: 题型:解答题
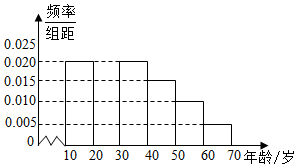 某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间的调查.这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”,否则称为“亚健康族”)人数及相应频率,得到统计表如表所示.
某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间的调查.这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”,否则称为“亚健康族”)人数及相应频率,得到统计表如表所示.| 组数 | 分组 | 亚健康族的人数 | 占本组的频率 |
| 第一组 | [10,20) | 100 | 0.5 |
| 第二组 | [20,30) | 195 | P |
| 第三组 | [30,40) | 120 | 0.6 |
| 第四组 | [40,50) | a | 0.4 |
| 第五组 | [50,60) | 30 | 0.3 |
| 第六组 | [60,70) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
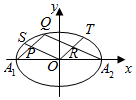 如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 5 | B. | 3+$\sqrt{5}$ | C. | 9 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com