
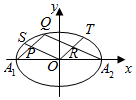
 如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 5 | B. | 3+$\sqrt{5}$ | C. | 9 | D. | 14 |
分析 设Q(x0,y0),则$\frac{{x}_{0}^{2}}{9}$+$\frac{{y}_{0}^{2}}{5}$=1,可得:${k}_{{A}_{2}Q}$•${k}_{{A}_{1}Q}$=-$\frac{{b}^{2}}{{a}^{2}}$.设直线OS,OT的方程分别为:y=k1x,y=k2x,则${k}_{{A}_{2}Q}$=k1,${k}_{{A}_{1}Q}$=k2.可得k1k2.直线方程与椭圆方程分别联立可得${x}_{S}^{2}$,${y}_{S}^{2}$;${x}_{T}^{2}$,${y}_{T}^{2}$.即可得出:|OS|2+|OT|2.
解答 解:设Q(x0,y0),则$\frac{{x}_{0}^{2}}{9}$+$\frac{{y}_{0}^{2}}{5}$=1,∴${y}_{0}^{2}$=$\frac{5}{9}(9-{x}_{0}^{2})$.
设直线OS,OT的方程分别为:y=k1x,y=k2x,
则${k}_{{A}_{2}Q}$=k1,${k}_{{A}_{1}Q}$=k2.
∵${k}_{{A}_{2}Q}$•${k}_{{A}_{1}Q}$=$\frac{{y}_{0}}{{x}_{0}+3}$$•\frac{{y}_{0}}{{x}_{0}-3}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-9}$=-$\frac{5}{9}$.
∴k1k2=-$\frac{5}{9}$.
联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,解得${x}_{S}^{2}$=$\frac{45}{5+9{k}_{1}^{2}}$,${y}_{S}^{2}$=$\frac{45{k}_{1}^{2}}{5+9{k}_{1}^{2}}$.
同理可得:${x}_{T}^{2}$=$\frac{45}{5+9{k}_{2}^{2}}$,${y}_{T}^{2}$=$\frac{45{k}_{2}^{2}}{5+9{k}_{2}^{2}}$.
∴|OS|2+|OT|2=${x}_{S}^{2}$+${y}_{S}^{2}$+${x}_{T}^{2}$+${y}_{T}^{2}$=$\frac{45}{5+9{k}_{1}^{2}}$+$\frac{45{k}_{1}^{2}}{5+9{k}_{1}^{2}}$+$\frac{45}{5+9{k}_{2}^{2}}$+$\frac{45{k}_{2}^{2}}{5+9{k}_{2}^{2}}$
=$\frac{45(1+{k}_{1}^{2})}{5+9{k}_{1}^{2}}$+$\frac{45(1+\frac{25}{81{k}_{1}^{2}})}{5+9×\frac{25}{81{k}_{1}^{2}}}$=$\frac{70+126{k}_{1}^{2}}{5+9{k}_{1}^{2}}$=14.
故选:D.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、平行四边形的性质,考查了推理能力与计算能力,属于难题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | c<a<b | C. | c<b<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
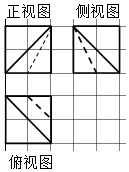 如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )
如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{19}{3}$ | C. | 6 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 10 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com