
| A. | 2 | B. | $\frac{7}{9}$ | C. | $\frac{15}{16}$ | D. | $\frac{17}{16}$ |
分析 求导f′(x)=$\frac{(3{x}^{2}+1)({x}^{4}+6{x}^{2}+1)-({x}^{3}+x)(4{x}^{3}+12x)}{({x}^{4}+6{x}^{2}+1)^{2}}$=$\frac{-({x}^{2}-1)^{3}}{{(x}^{4}+6{x}^{2}+1)^{2}}$,从而利用导数的正负确定函数的单调性,从而确定函数的最值即可.
解答  解:∵f(x)=$\frac{{x}^{3}+x}{{x}^{4}+6{x}^{2}+1}$+1,
解:∵f(x)=$\frac{{x}^{3}+x}{{x}^{4}+6{x}^{2}+1}$+1,
∴f′(x)=$\frac{(3{x}^{2}+1)({x}^{4}+6{x}^{2}+1)-({x}^{3}+x)(4{x}^{3}+12x)}{({x}^{4}+6{x}^{2}+1)^{2}}$
=$\frac{-({x}^{2}-1)^{3}}{{(x}^{4}+6{x}^{2}+1)^{2}}$,
故f(x)在(-∞,-1)上是减函数,
在(-1,1)上是增函数,在(1,+∞)上是减函数
且x→-∞时,f(x)→1;x→+∞时,f(x)→1;
而f(-1)=$\frac{-1-1}{1+6+1}$+1=$\frac{3}{4}$,
f(1)=$\frac{1+1}{1+6+1}$+1=$\frac{5}{4}$,
故f(-1)f(1)=$\frac{15}{16}$,
故选:C.
点评 本题考查了导数的综合应用及转化思想的应用,同时考查了分类讨论的思想应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | 3$\sqrt{2}$-1 | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
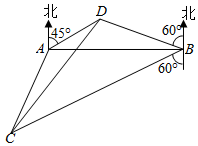 2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?
2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距5(3+$\sqrt{3}$)千米的两个观测点.现位于A点北偏东45°,B点北偏西60°的客船东方之星(D点)发出求救信号,位于B点南偏西60°且与B点相距20$\sqrt{3}$千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com