
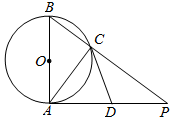
 已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.
已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.分析 (1)连接OC,OD,证明∠BAD+∠OCD=180°,可得四点O,A,D,C共圆;
(2)利用△ABP~△CBA及切割线的定理可证明:AC•AP=PC•AB.
解答 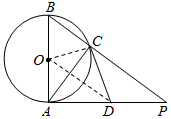 证明:(1)连接OC,OD,
证明:(1)连接OC,OD,
∵AB为⊙O的直径,可得∠BCA=90°,
在△ACP中,$CD=\frac{1}{2}AP=AD$,
∴∠DCA=∠DAC,
∵OA=OC,∴∠OCA=∠OAC,可知∠OCD=∠OCA+∠DCA=∠OAC+∠DCA=90°,
即∠BAD+∠OCD=180°,
∴四点O,A,D,C是共圆的…(5分)
(2)∵△ABP~△CBA,∴$\frac{AC}{AP}=\frac{AB}{PB}⇒\frac{PB}{AP}=\frac{AB}{AC}$,
又因为PA为圆O的切线,由切割线的定理可知AP2=PC•PB,即$\frac{AP}{PC}=\frac{PB}{AP}$,
代入可得$\frac{AP}{PC}=\frac{AB}{AC}⇒AP•AC=AB•PC$…(10分)
点评 本题考查四点共圆的证明,考查△ABP~△CBA及切割线的定理的运用,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x=2a,a∈P} | B. | {x|x=2a,a∈P} | C. | {x|x=a-1,a∈N} | D. | {x|x=a2,a∈N} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
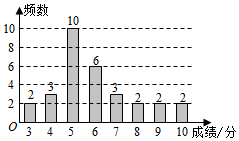 某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )
某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )| A. | me=m0=$\overline x$ | B. | me=m0<$\overline x$ | C. | me<m0<$\overline x$ | D. | m0<me<$\overline x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com