
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)求出K2=3.535>2.706,从而有90%的把握认为科目偏向与性别有关.
(2)在偏文科的学生中按分层抽样的方法选出6人,其中男生2人,分别设为A1,A2,女生4人分别设为B1,B2,B3,B4.由此利用列举法能求出在这6人中选取2人进行面对面交流求选出的2名学生是女生的概率.
解答 解:(1)∵${k^2}=\frac{{56{{({28×8-16×4})}^2}}}{44×12×32×24}=3.535>2.706$.
∴有90%的把握认为科目偏向与性别有关.
(2)在偏文科的学生中按分层抽样的方法选出6人,其中男生2人,分别设为A1,A2,
女生4人分别设为B1,B2,B3,B4.选出2人的基本事件为:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),
(A2,B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),
(B2,B3),(B2,B4),(B3,B4),共15个.
记“在这6人中选2人是女生”为事件A.
则事件A包含的基本事件有:
(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),共6个,
∴在这6人中选取2人进行面对面交流求选出的2名学生是女生的概率P(A)=$\frac{m}{n}=\frac{6}{15}=\frac{2}{5}$.
点评 本题考查独立检验的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,5] | B. | (-3,1) | C. | (-3,1] | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
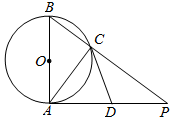 已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.
已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 售价(单位:元) | 23 | 21 | 20 |
| 日销量(单位:个) | 10 | 15 | 20 |
| 频数 | 4 | 14 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{3}x$ | B. | y=2x | C. | $y=±\sqrt{2}x$ | D. | $y=±\sqrt{3}x$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com