
 某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )
某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )| A. | me=m0=$\overline x$ | B. | me=m0<$\overline x$ | C. | me<m0<$\overline x$ | D. | m0<me<$\overline x$ |
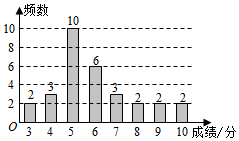
分析 30名学生的得分情况依次为得3分的有2人,得4分的有3人,得5分的有10人,得6分的有6人,得7分的有3人,得8分的有2人,得9分的有2人,得10分的有2人.由此能求出结果.
解答 解:由图可知,
30名学生的得分情况依次为得3分的有2人,得4分的有3人,得5分的有10人,
得6分的有6人,得7分的有3人,得8分的有2人,得9分的有2人,得10分的有2人.
中位数为第15、16个数,分别为5、6的平均数,即中位数me=5.5,
5出现的次数最多,故众数m0=5,
$\overline x=\frac{2×3+3×4+10×5+6×6+3×7+2×8+2×9+2×10}{30}≈5.97$,
所以m0<me<$\overline x$.
故选:D.
点评 本题考查分值的中位数为me,众数为m0,平均值为$\overline x$的大小的比较,是基础题,解题时要认真审题,注意条形图的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
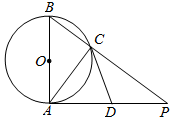 已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.
已知AB是⊙O的直径,AP是⊙O的切线,A为切点,BP与⊙O交于C点,AP的中点为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com