
分析 设∠BAD=α,∠CAD=β,由∠BAD+∠C=90°,可得α=90°-∠C,β=90°-∠B,由D为BC的中点,可得S△ABD=S△ACD,因此$\frac{1}{2}c•ADsinα=\frac{1}{2}b•ADsinβ$,
化为csinα=bsinβ,可得ccosC=bcosB,利用正弦定理即可得出.
解答 解:设∠BAD=α,∠CAD=β,∵∠BAD+∠C=90°,∴α=90°-∠C,β=90°-∠B,
∵D为BC的中点,∴S△ABD=S△ACD,∴$\frac{1}{2}c•ADsinα=\frac{1}{2}b•ADsinβ$,
∴csinα=bsinβ,∴ccosC=bcosB,由正弦定理得,sinCcosC=sinBcosB,
∴sin2C=sin2B,∴2∠B=2∠C或2B+2C=π,∴∠B=∠C或$∠B+∠C=\frac{π}{2}$(舍去),
∴∠B=∠C=$\frac{π}{6}$.
点评 本题考查了三角形面积计算公式、正弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
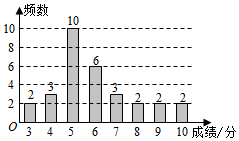 某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )
某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )| A. | me=m0=$\overline x$ | B. | me=m0<$\overline x$ | C. | me<m0<$\overline x$ | D. | m0<me<$\overline x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com