
分析 (1)由已知求得$tanφ=-\sqrt{3}$,结合φ的范围求得φ,再由已知求得ω得答案;
(2)直接由复合函数的单调性求得函数的增区间;
(3)由x的范围求得相位的范围,进一步求得sin($3x-\frac{π}{3}$)的范围得答案.
解答 解:(1)角φ的终边经过点$P(1,-\sqrt{3})$,∴$tanφ=-\sqrt{3}$,
∵$-\frac{π}{2}<φ<0$,∴$φ=-\frac{π}{3}$.
由|f(x1)-f(x2)|=4时,|x1-x2|的最小值为$\frac{π}{3}$,得$T=\frac{2π}{3}$,即$\frac{2π}{ω}=\frac{2π}{3}$,∴ω=3.
∴$f(x)=2sin(3x-\frac{π}{3})$;
(2)由$-\frac{π}{2}+2kπ≤3x-\frac{π}{3}≤\frac{π}{2}+2kπ$,得$-\frac{π}{18}+\frac{2kπ}{3}≤x≤\frac{5π}{18}+\frac{2kπ}{3}$,k∈Z,
∴函数f(x)的单调递增区间为$[{-\frac{π}{18}+\frac{2kπ}{3},}\right.\left.{\frac{5π}{18}+\frac{2kπ}{3}}]$(k∈Z);
(3 ) 当$x∈[{0,\frac{π}{3}}]$时,即0≤x≤$\frac{π}{3}$,则0≤3x≤π,
∴$-\frac{π}{3}≤3x-\frac{π}{3}≤\frac{2π}{3}$,
由函数单调性可得:$-\frac{\sqrt{3}}{2}≤sin(3x-\frac{π}{3})≤1$,
∴$-\sqrt{3}≤f(x)≤2$,
∴函数f(x)的值域为$[-\sqrt{3},2]$.
点评 本题考查三角恒等变换中的应用,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
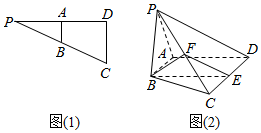 如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,构成四棱锥P-ABCD(如图2),且$\frac{PC}{PF}$=$\frac{CD}{CE}$=2
如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,构成四棱锥P-ABCD(如图2),且$\frac{PC}{PF}$=$\frac{CD}{CE}$=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com