
分析 直线C1的参数方程为$\left\{{\begin{array}{l}{x=1+t}\\{y=7+t}\end{array}}\right.(t$为参数),消去t化为普通方程:x-y+6=0.曲线C2的方程ρ=-2cosθ+2sinθ,即ρ2=-2ρcosθ+2ρsinθ,把ρ2=x2+y2,x=ρcosθ,y=ρsinθ代入即可得出直角坐标方程.求出圆心到直线的距离d,即可得出曲线C2上任意一点到直线C1距离的最小值=d-r.
解答 解:直线C1的参数方程为$\left\{{\begin{array}{l}{x=1+t}\\{y=7+t}\end{array}}\right.(t$为参数),消去t化为普通方程:x-y+6=0.
曲线C2的方程ρ=-2cosθ+2sinθ,即ρ2=-2ρcosθ+2ρsinθ,可得直角坐标方程:x2+y2=-2x+2y,配方化为:(x+1)2+(y-1)2=2,
可得圆心C2(-1,1),半径r=$\sqrt{2}$.
圆心到直线的距离d=$\frac{|-1-1+6|}{\sqrt{2}}$=2$\sqrt{2}$
曲线C2上任意一点到直线C1距离的最小值=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
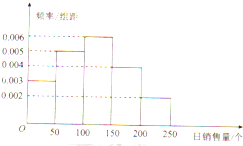 如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )
如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )| A. | 100 | B. | 113 | C. | 117 | D. | 125 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,D四点在同一圆上,AB∥CD,AD的延长线与BC的延长线交于E点.
如图,A,B,C,D四点在同一圆上,AB∥CD,AD的延长线与BC的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
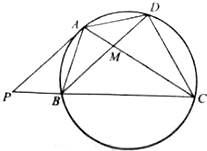 如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD
如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
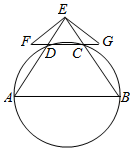
 如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com