
分析 根据用二分法求方程的近似解的方法,函数必须是连续函数,且函数在零点两侧的函数值异号,由此检验各个选项中的函数,作出判断.
解答 解:对于①因为在(0,1)上lnx<0,3x2>0,
所以3x2-lnx>0,在(0,1)上恒成立,故在(0,1)无解;
对于②设f(x)=x+lnx,f(1)=1>0,f($\frac{1}{e}$)=$\frac{1}{e}$+ln$\frac{1}{e}$=$\frac{1}{e}$-1<0,
∴f($\frac{1}{e}$)f(1)<0,
∴x+lnx=0在区间(0,1)内有实数解;
对于③,设f(x)=x3-3x2+3x-4,则f′(x)=3x2-6x+3=3(x-1)2≥0,
∴f(x)在(0,1)上单调递增,
∴f(0)=-4<0,f(1)=1-3+3-4=-3<0,
∴f(x)在(0,1)无零点,故x3-3x2+3x-4=0区间(0,1)内无实数解;
对于④设f(x)=x+$\frac{1}{x}$+2,则f′(x)=1-$\frac{1}{{x}^{2}}$<0在(0,1)上恒成立,
∴f(x)在(0,1)上单调递减,
∴f(1)=1+$\frac{1}{1}$+2=3,当x→0时,f(x)→+∞,
∴f(x)在(0,1)无零点,
故x+$\frac{1}{x}$=2中在区间(0,1)内无实数解.
故答案为:②
点评 本题主要考查用二分法求方程的近似解,注意用二分法求方程的近似解的条件,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
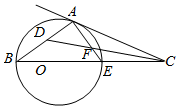 已知点C在圆O直径BE的延长线上,CA切圆O于A点,CD分别交AE、AB于点F、D,∠ADF=45°.
已知点C在圆O直径BE的延长线上,CA切圆O于A点,CD分别交AE、AB于点F、D,∠ADF=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com