
分析 (1)先逆用两角差的正弦公式化成正弦型函数的标准形式,然后利用周期公式T=$\frac{2π}{|ω|}$求ω的值,进而写出函数f(x)的解析式;
(2)利用余弦定理结合基本不等式求出cosB的范围,再根据B为三角形的内角求出B的范围,得出f(x)的定义域,从而求出f(x)的值域.
解答 解:(1)f(x)=$\sqrt{3}$sinωx•cosωx-cos2ωx
=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1+cos2ωx}{2}$
=sin(2ωx-$\frac{π}{6}$)-$\frac{1}{2}$;
由T=$\frac{2π}{2ω}$=$\frac{π}{2}$,解得ω=2,
所以函数f(x)的解析式为
f(x)=sin(4x-$\frac{π}{6}$)-$\frac{1}{2}$;
(2)因为b2=ac,
所以cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=$\frac{{a}^{2}{+c}^{2}}{2ac}$-$\frac{1}{2}$≥$\frac{2ac}{2ac}$-$\frac{1}{2}$=$\frac{1}{2}$,当且仅当a=c时取“=”;
又B为三角形内角,
所以0<B≤$\frac{π}{3}$,即0<x≤$\frac{π}{3}$,
所以-$\frac{π}{6}$<4x-$\frac{π}{6}$≤$\frac{7π}{6}$,
所以-$\frac{1}{2}$≤sin(4x-$\frac{π}{6}$)≤1,
所以-1≤sin(4x-$\frac{π}{6}$)-$\frac{1}{2}$≤$\frac{1}{2}$,
即函数f(x)的值域是[-1,$\frac{1}{2}$].
点评 本题考查了三角变换及解三角形的应用问题,解题的关键是化成正弦型函数的标准形式,把求角的范围转化成先求角余弦值的范围,是综合性题目.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
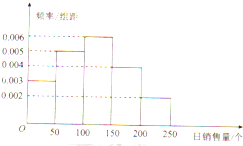 如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )
如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )| A. | 100 | B. | 113 | C. | 117 | D. | 125 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(0,\frac{1}{4})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
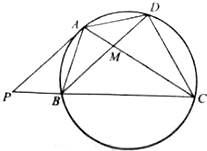 如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD
如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com