
分析 (1)利用同角三角函数的基本关系,求得g(t)的表达式.
(2)令t=sinx∈[-1,1],再利用二次函数的性质,求得g(t)=kt有且仅有一个实根时实数k的取值范围.
(3)令u=sinθ,u∈[-1,1],则由题意可得 g(u)=u2-6u+1=a-5u 有2个解,再利用二次函数的性质求得a的范围.
解答 解:(1)由已知有:f(x)=-cos2x-2t•sinx+2t2-6t+2=sin2x-2tsinx+2t2-6t+1=(sinx-t)2+t2-6t+1,
由于x∈R,∴-1≤sinx≤1,
∴当 t<-1时,则当sinx=-1时,$f{(x)_{min}}=2{t^2}-4t+2$;
当-1≤t≤1时,则当sinx=t时,$f{(x)_{min}}={t^2}-6t+1$;
当 t>1时,则当sinx=1时,$f{(x)_{min}}=2{t^2}-8t+2$;
综上,$g(t)=\left\{\begin{array}{l}2{t^2}-4t+2,t∈(-∞,-1)\\{t^2}-6t+1,t∈[-1,1]\\ 2{t^2}-8t+2,t∈(1,+∞)\end{array}\right.$.
(2)当-1≤t≤1时,g(t)=t2-6t+1,方程g(t)=kt,即:t2-6t+1=kt,
即方程 t2-(k+6)t+1=0在区间[-1,1]有且仅有一个实根,
令 q(t)=t2-(k+6)t+1,则有:q(-1)q(1)≤0,得(k+8)(k+4)≥0,
求得k∈(-∞,-8]∪[-4,+∞).
(3)令u=sinθ,u∈[-1,1],则由题意可得 g(u)=u2-6u+1=a-5u,
即关于u的方程u2-u+1=a 有2个根.
根据函数y=u2-u+1的图象的对称轴为x=$\frac{1}{2}$时,y=$\frac{3}{4}$,且当x=1时,y=1;当x=-1时,y=3,
∴$a=\frac{3}{4}$,或1<a<3.
点评 本题主要考查二次函数的性质,正弦函数的值域,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
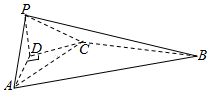 已知四棱锥P-ABCD如图所示,其中四边形ABCD是等腰梯形,且∠ADC+∠DAB=180°,AB=2AD=2DC=2BC=4,PA=PC,平面PAC⊥平面ABCD,点P到平面ABCD的距离为$\sqrt{3}$.
已知四棱锥P-ABCD如图所示,其中四边形ABCD是等腰梯形,且∠ADC+∠DAB=180°,AB=2AD=2DC=2BC=4,PA=PC,平面PAC⊥平面ABCD,点P到平面ABCD的距离为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
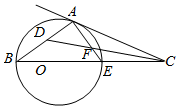 已知点C在圆O直径BE的延长线上,CA切圆O于A点,CD分别交AE、AB于点F、D,∠ADF=45°.
已知点C在圆O直径BE的延长线上,CA切圆O于A点,CD分别交AE、AB于点F、D,∠ADF=45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
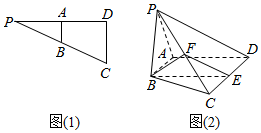 如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,构成四棱锥P-ABCD(如图2),且$\frac{PC}{PF}$=$\frac{CD}{CE}$=2
如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,构成四棱锥P-ABCD(如图2),且$\frac{PC}{PF}$=$\frac{CD}{CE}$=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
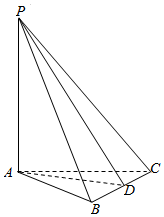 如图所示:三角形ABC是边长为2的等边三角形,PA⊥平面ABC,PA=3,D是BC的中点,
如图所示:三角形ABC是边长为2的等边三角形,PA⊥平面ABC,PA=3,D是BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 9 | C. | -9 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com