
分析 (1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,可得圆的直角坐标方程;
(2)求得A,B的直角坐标,即可得到直线AB的方程;求得AB的距离和圆C和半径,求得圆C到直线AB的距离,由圆C上的点到直线AB的最大距离为d+r,运用三角形的面积公式,即可得到所求最大值.
解答 解:(1)由ρ=2cosθ,可得:ρ2=2ρcosθ,所以x2+y2=2x
故在平面直角坐标系中圆的标准方程为:(x-1)2+y2=1 …(5分)
(2)在直角坐标系中A(0,3$\sqrt{3}$),B($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$)
所以|AB|=$\sqrt{(\frac{3}{2}-0)^{2}+(\frac{3\sqrt{3}}{2}-3\sqrt{3})^{2}}$=3,直线AB的方程为:$\sqrt{3}$x+y=3$\sqrt{3}$
所以圆心到直线AB的距离d=$\frac{|\sqrt{3}-3\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$,又圆C的半径为1,
所以圆C上的点到直线AB的最大距离为$\sqrt{3}$+1
故△ABP面积的最大值为S=$\frac{1}{2}×(\sqrt{3}+1)×3$=$\frac{3\sqrt{3}+3}{2}$ …(10分)
点评 本题考查极坐标方程和直角坐标方程的互化,直线和圆方程的运用,注意运用圆上的点到直线的距离的最值,考查运算求解能力,考查化归与转化思想等.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(0,\frac{1}{4})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=($\sqrt{2}$)n-1 | B. | an=($\sqrt{2}$)n | ||
| C. | an=$\left\{\begin{array}{l}{(\sqrt{2})^{n},n为奇数}\\{(\sqrt{2})^{n-1},n为偶数}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{(\sqrt{2})^{n-1},n为奇数}\\{(\sqrt{2})^{n},n为偶数}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
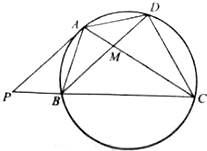 如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD
如图,PA为四边形ABCD外接圆的切线,CB的延长线交PA于点P,AC与BD相交于点M,PA∥BD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
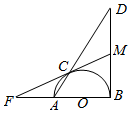 如图,AB为⊙O的直径,∠ABD=90°,线段AD交半圆于点C,过点C作半圆切线与线段BD交于点M,与线段BA延长线交于点F.
如图,AB为⊙O的直径,∠ABD=90°,线段AD交半圆于点C,过点C作半圆切线与线段BD交于点M,与线段BA延长线交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
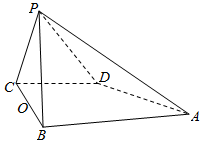 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=AB,△PBC为等边三角形,平面PBC⊥平面ABCD.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=AB,△PBC为等边三角形,平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}\overrightarrow{AC}$+$\frac{1}{3}$$\overrightarrow{AB}$ | B. | $\frac{1}{2}\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{AB}$ | C. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{1}{2}\overrightarrow{AB}$ | D. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{3}{2}$$\overrightarrow{AB}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com