
分析 (Ⅰ)求出抛物线的标准方程,根据抛物线y=ax2(a>0)的焦点到准线的距离为$\frac{1}{2}$,求出p的值,即可求出a的值;
(Ⅱ)运用中点坐标公式可得Q的坐标,运用两点的斜率公式,可得QA的斜率,求得抛物线对应函数的导数,可得切线的斜率,即可得证;
解答 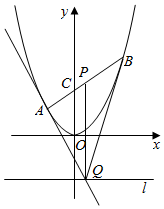 解:(Ⅰ)抛物线的标准方程为x2=$\frac{1}{a}$y,
解:(Ⅰ)抛物线的标准方程为x2=$\frac{1}{a}$y,
即2p=$\frac{1}{a}$,
∵抛物线y=ax2(a>0)的焦点到准线的距离为$\frac{1}{2}$,
∴p=$\frac{1}{2}$,即2p=$\frac{1}{a}$=1,
则a=1;
(Ⅱ)由(Ⅰ)得抛物线的标准方程为x2=y,
设直线AB:y=kx+c,与y=x2联立,得x2-kx-c=0,
设A(x1,y1),B(x2,y2),
则x1+x2=k,x1x2=-c,从而y1y2=x12x22=c2,
若P为线段AB的中点,则$\frac{{{x_1}+{x_2}}}{2}=\frac{k}{2}$,
故直线PQ:x=$\frac{k}{2}$,可得$Q({\frac{k}{2},-c})$.
设$A({x_1},x_1^2)$,kQA=$\frac{{{x}_{1}}^{2}+c}{{x}_{1}-\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{2({{x}_{1}}^{2}+c)}{{x}_{1}-{x}_{2}}$,
由(Ⅰ)可得x1x2=-c,即有x2=-$\frac{c}{{x}_{1}}$,
可得kQA=$\frac{2({{x}_{1}}^{2}+c)}{{x}_{1}-(-\frac{c}{{x}_{1}})}$=2x1,
由y=x2的导数为y′=2x,
可得过A的切线的斜率为2x1,
故直线QA与该抛物线有且仅有一个公共点;即QA为抛物线的切线.
同理可知QB也为抛物线的切线.
即QA,QB为抛物线的切线.
点评 本题考查抛物线的方程和性质,根据抛物线的定义求出抛物线的标准方程是解决本题的关键.联立直线和抛物线的方程,利用设而不求的思想,结合直线的斜率公式的运用,考查化简整理的运算能力,运算量较大,综合性较强.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
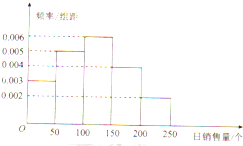 如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )
如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )| A. | 100 | B. | 113 | C. | 117 | D. | 125 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(0,\frac{1}{4})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
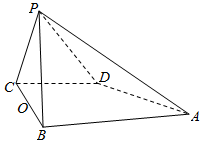 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=AB,△PBC为等边三角形,平面PBC⊥平面ABCD.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=AB,△PBC为等边三角形,平面PBC⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com