
分析 (1)求得h(x)导函数h'(x),代入求得f(x)的解析式,f(x)在区间(2,+∞)上单调递增,可知f′(x)≥0,在区间(2,+∞)上恒成立,即$a≤\frac{x^2}{x+1}$在x∈(2,+∞)上恒成立.构造辅助函数求导,利用导数求得函数的最小值,即可求得a的取值范围;
(2)由(1)求得F(x)的解析式.进一步化解,构造辅助函数,求导,利用导数求的函数的单调区间及最小值,即可求得F(x)≥$\frac{1}{2}$.
解答 解:(1)函数$h(x)=\frac{1}{3}{x^3}-a{x^2}+1$,h'(x)=x2-2ax,
函数f(x)=h'(x)-2alnx,
∴f(x)=x2-2ax-2alnx,
∵f(x)在区间(2,+∞)上单调递增,
∴$f'(x)=\frac{{2{x^2}-2ax-2a}}{x}≥0$在区间(2,+∞)上恒成立,
∴$a≤\frac{x^2}{x+1}$在x∈(2,+∞)上恒成立.
令$M(x)=\frac{x^2}{x+1}$,则$M'(x)=\frac{{2x(x+1)-{x^2}}}{{{{(x+1)}^2}}}=\frac{{{x^2}+2x}}{{{{(x+1)}^2}}}$,
当x∈(2,+∞)时,M'(x)>0,所以$M(x)=\frac{x^2}{x+1}>M(2)=\frac{4}{3}$,
∴实数a的取值范围为$(-∞,\frac{4}{3}]$.
(2)证明:$F(x)={x^2}-2ax-2alnx+{ln^2}x+2{a^2}=2[{a^2}-(x+lnx)a+\frac{{{x^2}+{{ln}^2}x}}{2}]$,
令$P(a)={a^2}-(x+lnx)a+\frac{{{x^2}+{{ln}^2}x}}{2}$,
则$P(a)={(a-\frac{x+lnx}{2})^2}-{(\frac{x+lnx}{2})^2}+\frac{{{x^2}+{{ln}^2}x}}{2}={(a-\frac{x+lnx}{2})^2}+{(\frac{x-lnx}{4})^2}≥{(\frac{x-lnx}{4})^2}$.
令Q(x)=x-lnx,则$Q'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,
显然Q(x)在区间(0,1)上单调递减,在区间[1,+∞)上单调递增,则Q(x)min=Q(1)=1,
则$P(a)≥\frac{1}{4}$,故$F(x)≥2×\frac{1}{4}=\frac{1}{2}$.
点评 本题考查函数的极值与导函数的关系,考查函数的单调性与导数的关系,函数与不等式、导数结合,考查计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x=2a,a∈P} | B. | {x|x=2a,a∈P} | C. | {x|x=a-1,a∈N} | D. | {x|x=a2,a∈N} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
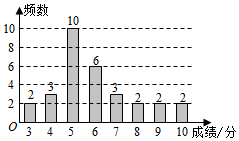 某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )
某机构在某一学校随机抽取30名学生参加环保知识测试,测试成绩(单位:分)如图所示,假设得分值的中位数为me,众数为m0,平均值为$\overline x$,则( )| A. | me=m0=$\overline x$ | B. | me=m0<$\overline x$ | C. | me<m0<$\overline x$ | D. | m0<me<$\overline x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(0,\frac{1}{4})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
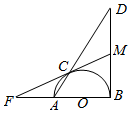 如图,AB为⊙O的直径,∠ABD=90°,线段AD交半圆于点C,过点C作半圆切线与线段BD交于点M,与线段BA延长线交于点F.
如图,AB为⊙O的直径,∠ABD=90°,线段AD交半圆于点C,过点C作半圆切线与线段BD交于点M,与线段BA延长线交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com