
���� ��1��������Բ�������ʹ�ʽ��a��b��c�Ĺ�ϵ�����a��b�������õ���Բ���̣�
��2��������ɵ�ֱ��l��y=1-x��������Բ���̣���ý��㣬��������ľ��빫ʽ���㼴�ɵõ�����
��3����ֱ��l��D��1��0���Ҵ�ֱ��x�ᣬ��A��1��y1����B��1��-y1�������AE�ķ��̣����M�����꣬����ֱ�ߵ�б�ʹ�ʽ���㼴�ɵõ�����ֵ��
��� �⣺��1��������ɵ�2c=2$\sqrt{2}$��$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$��
���a=$\sqrt{3}$��c=$\sqrt{2}$��b=$\sqrt{{a}^{2}-{c}^{2}}$=1��
������Բ�ķ���Ϊ$\frac{{x}^{2}}{3}$+y2=1��
��2��������ɵ�ֱ��l��y=1-x��������Բ���̿ɵ�
2x2-3x=0�����x=0��$\frac{3}{2}$����A��0��1����B��$\frac{3}{2}$��-$\frac{1}{2}$����
����|AB|=$\sqrt{��0-\frac{3}{2}��^{2}+��1+\frac{1}{2}��^{2}}$=$\frac{3\sqrt{2}}{2}$��
��3����ֱ��l��D��1��0���Ҵ�ֱ��x�ᣬ��A��1��y1����B��1��-y1����
AE�ķ���Ϊy-1=��1-y1����x-2������x=3�ɵ�M��3��2-y1����
����BM��б��Ϊk=$\frac{2-{y}_{1}-��-{y}_{1}��}{3-1}$=1��
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ��a��b��c�Ĺ�ϵ������ֱ�߷��̺���Բ�����������㣬����ֱ�ߵ�б�ʹ�ʽ������ľ��빫ʽ�����ã����ڻ����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{4}{9}$��1] | B�� | [$\frac{4}{9}$��1] | C�� | ��$\frac{4}{9}$��+�ޣ� | D�� | ��0��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
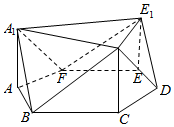 ��֪��ͼ������A1C1E1-ABCDEF�����DZ߳�Ϊ2�������Σ�AA1��CC1��EE1����Ϊ2�Ҷ���ֱ����棬
��֪��ͼ������A1C1E1-ABCDEF�����DZ߳�Ϊ2�������Σ�AA1��CC1��EE1����Ϊ2�Ҷ���ֱ����棬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
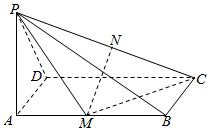 ��ͼ������P-ABCD�ĵ���Ϊ���Σ�PA�͵���ABCD����PA=AD��MΪAB���е㣮
��ͼ������P-ABCD�ĵ���Ϊ���Σ�PA�͵���ABCD����PA=AD��MΪAB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
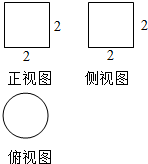
| A�� | 5�� | B�� | 4�� | C�� | 3�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
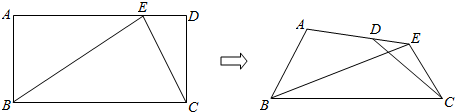
| A�� | $\frac{4}{5}$ | B�� | $\frac{5}{6}$ | C�� | $\frac{6}{7}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2cos1-sin1 | C�� | cos1-sin1 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com