
分析 由题意设|PC|:|CF|=1:t,由抛物线的焦半径公式比例关系求得P点坐标,则S△PFB=(1+t)2$\sqrt{2}$,根据三角形的面积公式,列方程即可求得t的值.
解答 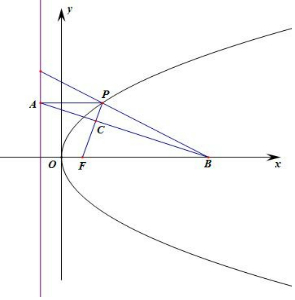 解:设抛物线E:y2=4x的焦点为F(1,0),准线x=-1,设P(xP,yP),
解:设抛物线E:y2=4x的焦点为F(1,0),准线x=-1,设P(xP,yP),
设|PC|:|CF|=1:t,则t丨PC丨=丨CF丨,丨AP丨=丨PF丨=xP+1,
由AB∥x轴,则丨AP丨:丨FB丨=|PC|:|CF|=$\frac{1}{t}$,即$\frac{1+{x}_{P}}{7-1}$=$\frac{1}{t}$,
则xP=$\frac{6-t}{t}$,yP=2$\sqrt{\frac{6-t}{t}}$,
由|PC|:|CF|=1:t,则S△PBC:S△FBC=1:t,
∴S△PFB=(1+t)2$\sqrt{2}$,
∴$\frac{1}{2}$×丨FB丨×yP=(1+t)2$\sqrt{2}$,即$\frac{1}{2}$×6×2$\sqrt{\frac{6-t}{t}}$=(1+t)2$\sqrt{2}$,
整理得:2t3+4t2+11t-54=0,解得:t=2,
∴|PC|:|CF|=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查抛物线的性质,考查相似三角形的性质,考查数形结合思想,考查计算能力,属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
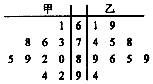 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com