
| A. | (-∞,-2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (1,2) |
分析 根据函数f(x)的解析式,列出不等式组求出解集即可.
解答 解:函数f(x)=$\frac{lg({x}^{2}-1)}{\sqrt{{x}^{2}-x-2}}$,
∴$\left\{\begin{array}{l}{{x}^{2}-1>0}\\{{x}^{2}-x-2>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x<-1或x>1}\\{x<-1或x>2}\end{array}\right.$,
即x<-1或x>2;
∴f(x)的定义域为(-∞,-1)∪(2,+∞).
故选:C.
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
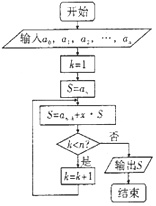 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )
秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )| A. | 248 | B. | 258 | C. | 268 | D. | 278 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
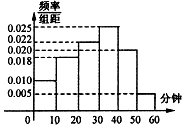 北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.| 非围棋迷 | 围棋迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(x2≥k0) | 0.05 | 0.010 |
| k0 | 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com