
【题目】某电子产品生产企业生产一种产品,原计划每天可以生产![]() 吨产品,每吨产品可以获得净利润
吨产品,每吨产品可以获得净利润![]() 万元,其中
万元,其中![]() ,由于受市场低迷的影响,该企业的净利润出现较大幅度下滑.为提升利润,该企业决定每天投入20万元作为奖金刺激生产.在此方案影响下预计每天可增产
,由于受市场低迷的影响,该企业的净利润出现较大幅度下滑.为提升利润,该企业决定每天投入20万元作为奖金刺激生产.在此方案影响下预计每天可增产![]() 吨产品,但是受原材料数量限制,增产量不会超过原计划每天产量的四分之一.试求在每天投入20万元奖金的情况下,该企业每天至少可获得多少利润(假定每天生产出来的产品都能销售出去).
吨产品,但是受原材料数量限制,增产量不会超过原计划每天产量的四分之一.试求在每天投入20万元奖金的情况下,该企业每天至少可获得多少利润(假定每天生产出来的产品都能销售出去).
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
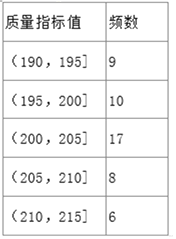
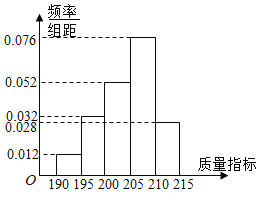
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市甲、乙两地为了争创“市级文明城市”,现市文明委对甲、乙两地各派10名专家进行打分评优,所得分数情况如下茎叶图所示.
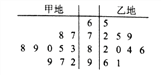
(1)分别计算甲、乙两地所得分数的平均值,并计算乙地得分的中位数;
(2)从乙地所得分数在![]() 间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在
间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在![]() 间的概率;
间的概率;
(3)在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性,求这2份成绩都是来自甲地的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中![]() 为实数集,
为实数集,![]() 为有理数集,则关于函数
为有理数集,则关于函数![]() 有如下四个命题:①
有如下四个命题:①![]() ;②函数
;②函数![]() 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;④存在三个点
恒成立;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中真命题的个数有( )
为等边三角形.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且
且![]() ,函数
,函数![]() 在点
在点![]() 处的切线过点
处的切线过点 ![]() .
.
(1) 求![]() 满足的关系式,并讨论函数
满足的关系式,并讨论函数![]() 的单调区间;
的单调区间;
(2)已知![]() ,若函数
,若函数![]() 在
在![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com