
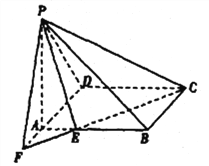
【题目】在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 平面
平面![]() ,
, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),
),![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() ;
;
(2)求证:在线段![]() 上可以分别找到两点
上可以分别找到两点![]() ,
, ![]() ,使得直线
,使得直线![]() 平面
平面![]() ,并分别求出此时
,并分别求出此时![]() 的值.
的值.
【答案】(1)见解析;(2)证明见解析, ![]() ,
, ![]() .
.
【解析】试题分析:(1)由题意易证![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则此时满足直线
,则此时满足直线![]() 平面
平面![]() . 在
. 在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,所以
,所以![]() .在
.在![]() 中,由
中,由 ,得
,得![]() 所以
所以 .
.
试题解析:
(1)证明:因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为底面![]() 是矩形,所以
是矩形,所以![]()
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)如图所示,取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则此时满足直线
,则此时满足直线![]() 平面
平面![]() .
.

由(1)得, ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]()
![]()
因为![]() 平面
平面![]() ,所以
,所以![]()
又因为![]() 是等腰三角形,所以
是等腰三角形,所以![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
易知![]() ,下面求解
,下面求解![]() :
:
因为![]() ,
, ![]() ,所以可设
,所以可设![]() ,则
,则![]() ,
, ![]() .
.
在等腰直角三角形![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
因为![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]()
![]() 的平面图如图所示:
的平面图如图所示:

在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,
,
所以![]() .
.
在![]() 中,由
中,由 ,得
,得![]() 所以
所以 .
.
综上,在线段![]() 上可以分别找到两点
上可以分别找到两点![]() ,
, ![]() ,使得直线
,使得直线![]() 平面
平面![]() ,
,
并且此时![]() ,
, ![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意
对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“以
是“以![]() 为界的类斜率函数”.
为界的类斜率函数”.
(1)试判断函数![]() 是否为“以
是否为“以![]() 为界的类斜率函数”;
为界的类斜率函数”;
(2)若实数![]() ,且函数
,且函数![]() 是“以
是“以![]() 为界的类斜率函数”,求
为界的类斜率函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1,(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(x2﹣x+a)的定义域为R,若p∨q为真p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,BC⊥PB,△BCD为等边三角形,PA=BD= ![]() ,AB=AD,E为PC的中点.
,AB=AD,E为PC的中点. 
(1)求证:BC⊥AB;
(2)求AB的长;
(3)求平面BDE与平面ABP所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|a﹣3<x<a+3},B={x|x2﹣2x﹣3>0}.
(1)若a=3,求A∩B,A∪B;
(2)若A∪B=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)判断并证明f(x)在(﹣∞,+∞)上的单调性;
(3)若对任意实数t∈R,不等式f(kt2﹣kt)+f(2﹣kt)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点. 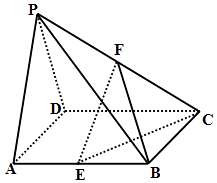
(1)求证:EF∥平面PAD;
(2)求三棱锥B﹣EFC的体积;
(3)求二面角P﹣EC﹣D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足在(﹣∞,0)上为增函数且f(﹣1)=0,则不等式xf(x)>0的解集为( )
A.(﹣∞,﹣1)∪(1,+∞)
B.(﹣1,0)∪(0,1)
C.(﹣1,0)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com