
【题目】若函数![]() 对任意
对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“以
是“以![]() 为界的类斜率函数”.
为界的类斜率函数”.
(1)试判断函数![]() 是否为“以
是否为“以![]() 为界的类斜率函数”;
为界的类斜率函数”;
(2)若实数![]() ,且函数
,且函数![]() 是“以
是“以![]() 为界的类斜率函数”,求
为界的类斜率函数”,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣x2+x.
x3﹣x2+x.
(1)求函数f(x)在[﹣1,2]上的最大值和最小值;
(2)若函数g(x)=f(x)﹣4x,x∈[﹣3,2],求g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2(a>0,且a≠1),若g(2)=a,则f(2)的值为(
A.![]()
B.2
C.![]()
D.a2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少? 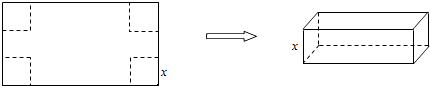
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 平面
平面![]() ,
, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),
),![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
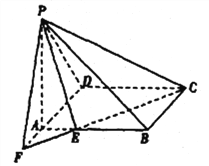
(1)求证: ![]() ;
;
(2)求证:在线段![]() 上可以分别找到两点
上可以分别找到两点![]() ,
, ![]() ,使得直线
,使得直线![]() 平面
平面![]() ,并分别求出此时
,并分别求出此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com