
【题目】已知函数![]() .
.
(1)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(2)求当![]() 时,
时, ![]() 恒成立的
恒成立的![]() 的取值范围,并证明
的取值范围,并证明![]()
![]() .
.
【答案】(1)a![]() e (2)见解析
e (2)见解析
【解析】试题分析:(1) 函数![]() 有两个不同的零点,等价于
有两个不同的零点,等价于![]() =
=![]() 在
在
(![]() ,+
,+![]() )上有两实根,利用导数研究函数
)上有两实根,利用导数研究函数![]() 的单调性,结合函数图象即可得结果;(2)结合(1)可得
的单调性,结合函数图象即可得结果;(2)结合(1)可得![]() <
<![]() ,令
,令![]() ,
, ![]()
![]() ,各式相加,化简即可得结果.
,各式相加,化简即可得结果.
试题解析:(1) f(x)有两个零点, ![]()
![]()
![]() 在(
在(![]() ,+
,+![]() )上有两实根,显然a
)上有两实根,显然a![]()
![]() =
=![]() ,令g(x)=
,令g(x)= ![]() , g/(x)=
, g/(x)= ![]() ,令g/(x)=0,x
,令g/(x)=0,x![]()
∴g(x)在(0, ![]() )单调递增,在(
)单调递增,在(![]() ,+
,+![]() )单调递减,又g(
)单调递减,又g(![]() )=
)=![]() ,x>1时g(x)>0.且
,x>1时g(x)>0.且![]() g(x)
g(x) ![]() 0
0
∴![]() =
=![]() 有两根须0<
有两根须0<![]() <
<![]() , ∴a
, ∴a![]() e
e
(2)![]() x2-alnx
x2-alnx![]() 0恒成立,即x2>2alnx对x>1恒成立.当a
0恒成立,即x2>2alnx对x>1恒成立.当a![]() 时,显然满足。
时,显然满足。
当a>![]() 时,
时, ![]() >
>![]() ,由(1)知,(g(x))MAX=
,由(1)知,(g(x))MAX=![]() ,
,![]() , ∴0<a<e
, ∴0<a<e
综上![]() x2-alnx
x2-alnx![]() 0对x>1恒成立的a的范围为a<e
0对x>1恒成立的a的范围为a<e
令a=2,则![]() x2-2lnx
x2-2lnx![]() 0对x>1恒成立,即lnx<
0对x>1恒成立,即lnx<![]() x2,令x=
x2,令x=![]() ,k=2,3,4,…,n
,k=2,3,4,…,n
lnk<![]() k,ln2
k,ln2![]() , ln3
, ln3![]() , ln4
, ln4![]() ,…,lnn<
,…,lnn<![]() n,
n,
∴ln2+ ln3+ ln4+…+ lnn<![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上. 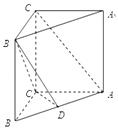
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当 ![]() =
= ![]() 时,求二面角B﹣CD﹣B1的余弦值.
时,求二面角B﹣CD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意
对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“以
是“以![]() 为界的类斜率函数”.
为界的类斜率函数”.
(1)试判断函数![]() 是否为“以
是否为“以![]() 为界的类斜率函数”;
为界的类斜率函数”;
(2)若实数![]() ,且函数
,且函数![]() 是“以
是“以![]() 为界的类斜率函数”,求
为界的类斜率函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加装修费2万元,现把写字楼出租,每年收入租金30万元.
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案:
①年平均利润最大时,以50万元出售该楼;
②纯利润总和最大时,以10万元出售该楼;
问选择哪种方案盈利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|0< ![]() ≤1},B={y|y=(
≤1},B={y|y=( ![]() )x , 且x<﹣1}
)x , 且x<﹣1}
(1)若集合C={x|x∈A∪B,且xA∩B},求集合C;
(2)设集合D={x|3﹣a<x<2a﹣1},满足A∪D=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1,(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(x2﹣x+a)的定义域为R,若p∨q为真p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)判断并证明f(x)在(﹣∞,+∞)上的单调性;
(3)若对任意实数t∈R,不等式f(kt2﹣kt)+f(2﹣kt)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com