
【题目】已知f(x)为偶函数,当x≥0时,f(x)=﹣(x﹣1)2+1,则满足f[f(a)+ ![]() ]=
]= ![]() 的实数a的个数为( )
的实数a的个数为( )
A.2
B.4
C.6
D.8
【答案】C
【解析】解:设t=f(a)+ ![]() ,
,
则条件等价为f(t)= ![]() ,
,
若x≤0,则﹣x≥0,
∵当x≥0时,f(x)=﹣(x﹣1)2+1,
∴当﹣x≥0时,f(﹣x)=﹣(﹣x﹣1)2+1=﹣(x+1)2+1,
∵f(x)为偶函数,
∴f(﹣x)=﹣(x+1)2+1=f(x),
即f(x)=﹣(x+1)2+1,x≤0,
作出函数f(x)的图象如图:
当x≥0时,由﹣(x﹣1)2+1= ![]() ,得(x﹣1)2=
,得(x﹣1)2= ![]() ,则x=1+
,则x=1+ ![]() 或x=1﹣
或x=1﹣ ![]() ,
,
∵f(x)为偶函数,
∴当x<0时,f(x)= ![]() 的解为x3=﹣1﹣
的解为x3=﹣1﹣ ![]() ,x4=﹣1+
,x4=﹣1+ ![]() ;
;
综上所述,f(t)= ![]() 得解为t1=1+
得解为t1=1+ ![]() 或t2=1﹣
或t2=1﹣ ![]() ,t3=﹣1﹣
,t3=﹣1﹣ ![]() ,t4=﹣1+
,t4=﹣1+ ![]() ;
;
由t=f(a)+ ![]() 得,
得,
若t1=1+ ![]() ,则f(a)+
,则f(a)+ ![]() =1+
=1+ ![]() ,即f(a)=
,即f(a)= ![]() +
+ ![]() >1,此时a无解,
>1,此时a无解,
若t2=1﹣ ![]() ,则f(a)+
,则f(a)+ ![]() =1﹣
=1﹣ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() ﹣
﹣ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
若t3=﹣1﹣ ![]() ,则f(a)+
,则f(a)+ ![]() =﹣1﹣
=﹣1﹣ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() ﹣
﹣ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
若t4=﹣1+ ![]() ,则f(a)+
,则f(a)+ ![]() =﹣1+
=﹣1+ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() +
+ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
故共有2+2+2=6个解.
故选:C.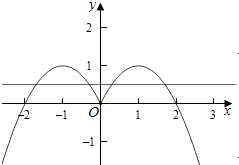
利用换元法将函方程转化为f(t)= ![]() ,利用数形结合进行求解即可.
,利用数形结合进行求解即可.


科目:高中数学 来源: 题型:
【题目】已知R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2(a>0,且a≠1),若g(2)=a,则f(2)的值为(
A.![]()
B.2
C.![]()
D.a2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少? 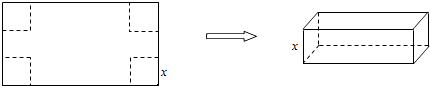
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数y= ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②若lna<1成立,则a的取值范围是(﹣∞,e);
③函数f(x)=ax+1﹣2(a>0,a≠1)的图象过定点(﹣1,﹣1);
④方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6﹣ax)(a>0,a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位正方体ABCD﹣A1B1C1D1中,O是B1D1的中点,如图建立空间直角坐标系. 
(1)求证:B1C∥平面ODC1;
(2)求异面直线B1C与OD夹角的余弦值;
(3)求直线B1C到平面ODC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线x﹣2y=0上.
(1)若圆C与y轴的正半轴相切,且该圆截x轴所得弦的长为2 ![]() ,求圆C的标准方程;
,求圆C的标准方程;
(2)在(1)的条件下,直线l:y=﹣2x+b与圆C交于两点A,B,若以AB为直径的圆过坐标原点O,求实数b的值;
(3)已知点N(0,3),圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使MN=2MO(O为坐标原点),求圆心C的纵坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com