
分析 (1)求导数,利用曲线y=f(x)在x=1处的切线与直线y=ex-1平行,求出a,可得切点坐标,即可求此切线方程
(2)分类讨论,求导数,利用极值的定义,可得函数g(x)在定义域内的极值点;
(3)由题意,等价于f(x)在x∈[1,+∞)上为增函数,从而a≤x2+x在x∈[1,+∞)上恒成立,即可求a的取值范围.
解答 解:(1)函数f(x)=ex+lnx+$\frac{a}{x}$,a∈R的导数f′(x)=ex+$\frac{1}{x}-\frac{a}{{x}^{2}}$,
∵曲线y=f(x)在x=1处的切线与直线y=ex-1平行,∴f′(1)=e,
即e+1-a=e,解得a=1.∴f(x)=ex+lnx+$\frac{1}{x}$,f(1)=e+1
即切点为(1,e+1),所以切线方程为y-(e+1)=e(x-1),
∴y=ex+1为所求.
(2)当a=0时,函数g(x)=f(x)-$\frac{1}{2b}$x2-ex(b∈R,b≠0),整理得g(x)=lnx-$\frac{1}{2b}{x}^{2}$,定义域为x∈(0,+∞),
g′(x)=$\frac{1}{x}-\frac{x}{b}=\frac{b-{x}^{2}}{bx}$,
①当b<0时,∴g′(x)>0恒成立,∴g(x)在x∈(0,+∞)上为增函数,∴g(x)在定义域内无极值;
②当b>0时,令g′(x)=0,∴x=$\sqrt{b}$或x=-$\sqrt{b}$(舍去),
x$∈(0,\sqrt{b})$时,g′(x)>0,x$∈(\sqrt{b},+∞)$时,g′(x)<0,
∴g(x)在(0,$\sqrt{b}$)递增,在($\sqrt{b}$,+∞)递减,∴g(x)的极大值点为$\sqrt{b}$,无极小值点;
综上:当b<0时,g(x)在定义域内无极值;b>0时,g(x)的极大值点为$\sqrt{b}$,无极小值点.
(3)h(x)=f(x)-ex=lnx+$\frac{a}{x}$.
?x1,x2∈[1,+∞),且x1<x2,都有h(x1)-h(x2)<x2-x1成立,
??x1,x2∈[1,+∞),且x1<x2,都有h(x1)+x1<h(x2)+x2成立.
??x1,x2∈[1,+∞),且x1<x2,都有lnx1+$\frac{a}{{x}_{1}}$+x1<lnx2+$\frac{a}{{x}_{2}}$+x2成立.
令F(x)=lnx+$\frac{a}{x}+x$,即F(x1)<F(x2),等价于F(x)在x∈[1,+∞)上为增函数,
∴F′(x)=$\frac{1}{x}+1-\frac{a}{{x}^{2}}=\frac{{x}^{2}+x-a}{{x}^{2}}$≥0在x∈[1,+∞)上恒成立,
即a≤x2+x在x∈[1,+∞)上恒成立,
令y=x2+x,只需a≤ymin即可.∵y在x∈[1,+∞)上为增函数,
∴当x=1时,ymin=2,∴a≤2.
点评 本题考查导数知识的综合运用,考查导数的几何意义、函数的极值、恒成立问题,考查学生分析解决问题的能力,知识综合性强.属于难题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
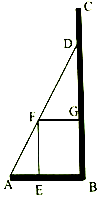 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com