
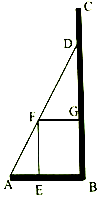
 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.分析 (1)求出△ABD的面积为,设正方形BEFG的边长为t,利用三角形的相似求出S2,然后求出S1;
(2)由(1)$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1,通过tanθ∈(0,+∞),通过基本不等式推出,当θ=$\frac{π}{4}$时,“规划和谐度”有最小值,最小值是1.
解答 解:(1)∵BD=atanθ,
∴△ABD的面积为$\frac{1}{2}{a}^{2}tanθ$($θ∈(0,\frac{π}{2})$)…(2分)
设正方形BEFG的边长为t,
则由$\frac{FG}{AB}=\frac{DG}{DB}$得$\frac{t}{a}=\frac{atanθ-t}{atanθ}$,∵t=$\frac{atanθ}{1+tanθ}$,…(4分)
∴S2=$\frac{{a}^{2}ta{n}^{2}θ}{(1+tanθ)^{2}}$,
∴S1=$\frac{1}{2}{a}^{2}tanθ$-S2=$\frac{1}{2}{a}^{2}tanθ$-$\frac{{a}^{2}ta{n}^{2}θ}{(1+tanθ)^{2}}$,…(6分)
(2)由(1)$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1,…(8分)
∵tanθ∈(0,+∞),
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1=$\frac{1}{2}$(tanθ+$\frac{1}{tanθ}$≥1,…(10分)
当且仅当tanθ=1时取等号,此时θ=$\frac{π}{4}$.
∴当θ=$\frac{π}{4}$时,“规划和谐度”有最小值,最小值是1.…(12分)
点评 本题考查解三角形的实际应用,基本不等式的应用,考查计算能力.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,n?α,则m∥α | B. | 若l∥n,m⊥n,则l∥m | ||
| C. | 若l⊥α,m⊥β,且l⊥m,则α⊥β | D. | 若α⊥β,α∩β=m,且m⊥n,则n⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com