
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
分析 利用辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,放到正弦函数的增减区间上,解不等式得函数的单调区间;根据对称轴方程求解对称即可.
解答 解:函数f(x)=sin(2x+$\frac{π}{6}$)+$\sqrt{3}$cos(2x+$\frac{π}{6}$),
化简可得:f(x)=sin(2x+$\frac{π}{6}$+$\frac{π}{3}$)=cos2x.
根据余弦函数的图象和性质,2kπ≤2x≤2kπ+π,
可得:$kπ≤x≤kπ+\frac{π}{2}$
∴递减区间为[kπ,$kπ+\frac{π}{2}$],k∈Z.
∵对称轴方程2x=kπ,k∈Z.
∴函数的对称轴方程为x=$\frac{π}{2}k$,k∈Z.
故选D
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (-1,2) | D. | (1+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
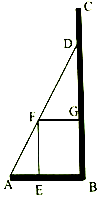 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com