
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 16个 |
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{l}{6}$)3π | B. | ($\frac{l}{3}$)3π | C. | ($\frac{l}{4}$)3π | D. | $\frac{1}{4}$($\frac{l}{4}$)3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
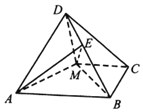 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
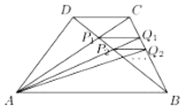 梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)
梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com