
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
分析 (1)由题意可知,X=0,1,2,3,且每个男性在这一时间段以看书为休闲方式的概率为$P=\frac{10}{30}=\frac{1}{3}$,随机变量X服从二项分布,运用独立重复试验公式求出概率后列出分布列,运用二项分布公式求X的期望;
(2)根据计算出的临界值,同临界值表进行比较,得到有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系.
解答 解:(1)由题意可知,X=0,1,2,3,
且每个男性在这一时间段以看书为休闲方式的概率为$P=\frac{10}{30}=\frac{1}{3}$,
根据题意可得X~B(3,$\frac{1}{3}$),∴$P(X=k)=C_3^k{(\frac{2}{3})^{3-k}}{(\frac{1}{3})^k}$,k=0,1,2,3,
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{4}{9}$ | $\frac{2}{9}$ | $\frac{1}{27}$ |
点评 本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
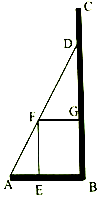 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com