
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
分析 利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律求得所得函数的解析式,再利用三角函数的奇偶性、单调性,以及它的图象的对称性,逐一判断各个选项是否正确,从而得出结论.
解答 解:把函数f(x)=2sin(2x+$\frac{π}{3}$+φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{2}$个单位后,
得到 y=2sin(2x+$\frac{π}{3}$+φ+π)=-2sin(2x+$\frac{π}{3}$+φ)的图象,
再根据所得关于y轴对称,可得$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,∴φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{3}$+φ)=2cos2x.
由于f(x+$\frac{π}{4}$)=2cos(2x+$\frac{π}{2}$)=-sin2x是奇函数,故A正确;
当x=$\frac{π}{4}$时,f(x)=0,故($\frac{π}{4}$,0)是f(x)的图象的一个对称中心,故B正确;
在$({-\frac{3π}{4},-\frac{π}{4}})$上,2x∈(-$\frac{3π}{2}$,-$\frac{π}{2}$),f(x)没有单调性,故C不正确;
在(0,$\frac{π}{2}$)上,2x∈(0,π),f(x)单调递减,故D正确,
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,三角函数的奇偶性、单调性,以及它的图象的对称性,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
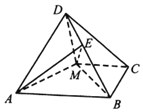 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
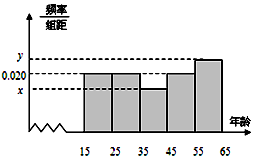 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.| 组号 | 分组 | 喜爱人数 | 喜爱人数占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65) | 20 | 0.80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com