
 ij���Ļ�����Ϊ���˽Ȿ������Ե��صط�Ϸ���Ƿ�ϲ������15-65�����Ⱥ�����������n�ˣ��õ����µ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ��
ij���Ļ�����Ϊ���˽Ȿ������Ե��صط�Ϸ���Ƿ�ϲ������15-65�����Ⱥ�����������n�ˣ��õ����µ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ��| ��� | ���� | ϲ������ | ϲ������ռ�����Ƶ�� |
| ��1�� | [15��25�� | a | 0.10 |
| ��2�� | [25��35�� | b | 0.20 |
| ��3�� | [35��45�� | 6 | 0.40 |
| ��4�� | [45��55�� | 12 | 0.60 |
| ��5�� | [55��65�� | 20 | 0.80 |
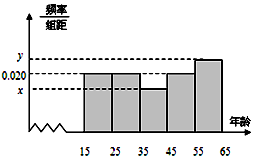
���� �����ɱ���֪��3��4����������ٸ���Ƶ�ʷֲ�ֱ��ͼ֪��1��2���������
������������͵�5����������Ӷ����a��b��n��x��y��ֵ��
�������÷ֲ����ԭ�������1��2��3��Ӧ��ȡ��������
����������֪X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��
д��X�ķֲ��У�������ѧ����ֵ��
��� �⣺�����ɱ���֪��3�������Ϊ$\frac{6}{0.40}$=15��
��4�������Ϊ$\frac{12}{0.60}$=20��
�ٸ���Ƶ�ʷֲ�ֱ��ͼ��֪��1�顢��2���������Ϊ20��
�ҳ�������Ϊ $n=\frac{20}{0.02��10}=100$��
���Ե�5�������Ϊ100-20-20-15-20=25��
��a=0.1��20=2��b=20��0.20=4��
$x=\frac{{\frac{15}{100}}}{10}=0.015$��.$y=\frac{{\frac{25}{100}}}{10}=0.025$������4�֣�
������Ϊ��1��2��3��ϲ���ط�Ϸ����������Ϊ2��4��6��
�÷ֲ���������������г�ȡ6�ˣ�
��1��Ӧ��ȡ1�ˣ���2��Ӧ��ȡ2�ˣ���3��Ӧ��ȡ3�ˣ�
���������⣬X�Ŀ���ȡֵ��0��1��2��
��$P��X=0��=\frac{C_3^2}{C_6^2}=\frac{1}{5}$��
$P��X=1��=\frac{C_3^1C_3^1}{C_6^2}=\frac{3}{5}$��
P��X=2��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ����ɢ����������ķֲ�������ѧ�����ļ������⣬���ۺ��⣮


 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��{x+\frac{��}{4}}��$���溯�� | B�� | $��{\frac{��}{4}��0}��$Ϊf��x����һ���Գ����� | ||
| C�� | f��x����$��{-\frac{3��}{4}��-\frac{��}{4}}��$�ϵ������� | D�� | f��x���ڣ�0��$\frac{��}{2}$���ϵ����ݼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-5��5] | B�� | [-5$\sqrt{2}$��5$\sqrt{2}$] | C�� | [-10��10] | D�� | [-10$\sqrt{2}$��10$\sqrt{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��y����Ϊ0 | B�� | x��y��x��y����Ϊ0 | C�� | x��y��x��y����Ϊ0 | D�� | x��y����Ϊ0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com