
分析 (1)求出导函数,通过当a≤0时,当a<0时,判断导函数的符号,推出函数的单调区间.
(2)由(1)可得:对a分类讨论,利用其单调性即可得出:方程f(x)=a的根的个数.
(3)$xf(x)≥{x^3}-\frac{5a+3}{2}{x^2}+3ax-1+m$,即$x({{e^x}-ax})≥{x^3}-\frac{5a+3}{2}{x^2}+3ax-1+m$对任意x∈[0,+∞)恒成立,因此$m≤x{e^x}-{x^3}+\frac{{3({a+1})}}{2}{x^2}-3ax+1=x({{e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a})+1$对任意x∈[0,+∞)恒成立.令$g(x)={e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a$,x∈[0,+∞),因为m的最大值为1,可知:$g(x)={e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a≥0$恒成立.必需g(0)=1-3a≥0,a$≤\frac{1}{3}$,则$-1≤a≤\frac{1}{3}$.g′(x)=ex-2x+$\frac{3(a+1)}{2}$=h(x).利用导数研究函数h(x)的单调性最值可得g(x)的单调性极值与最值.
解答 解:(1)因为f(x)=ex-ax,所以f′(x)=ex-a.
当a≤0时,f′(x)=ex-a>0,所以f(x)在(-∞,+∞)上单调递增.
当a<0时,令f′(x)=ex-a>0,得x>lna令,f′(x)=ex-a<0得x<1na,
所以f(x)在(-∞,1na)上单调递减;在(1na,+∞)上单调递增.
(2)由(1)可得:①当a<0时,函数f(x)在R上单调递增.
x→+∞时,f(x)→+∞;x→-∞时,f(x)→-∞.
因此此时方程f(x)=a的根的个数为1.
②a=0时,f(x)=ex>0,此时方程f(x)=a的根的个数为0.
③当a>0时,函数f(x)的单调递减区间是(-∞,lna);函数f(x)单调递增区间是[lna,+∞).
可得函数f(x)的极小值即最小值为:f(x)min=f(lna)=a-alna,
因此a=1时,f(x)min=f(0)=1,∴此时方程f(x)=a的根的个数为1.
a>1时,f(x)min=f(lna)=a-alna<a,∴此时方程f(x)=a的根的个数为2.
0<a<1时,f(x)min=f(lna)=a-alna>a,∴此时方程f(x)=a的根的个数为0.
综上可得:①当a<0时,此时方程f(x)=a的根的个数为1.
②a=0时,此时方程f(x)=a的根的个数为0.
③当a>0时,a=1时,此时方程f(x)=a的根的个数为1.
a>1时,此时方程f(x)=a的根的个数为2.
0<a<1时,此时方程f(x)=a的根的个数为0.
(3)$xf(x)≥{x^3}-\frac{5a+3}{2}{x^2}+3ax-1+m$,即$x({{e^x}-ax})≥{x^3}-\frac{5a+3}{2}{x^2}+3ax-1+m$
对任意x∈[0,+∞)恒成立,
所以$m≤x{e^x}-{x^3}+\frac{{3({a+1})}}{2}{x^2}-3ax+1=x({{e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a})+1$
对任意x∈[0,+∞)恒成立.
令$g(x)={e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a$,x∈[0,+∞),因为m的最大值为1,
所以$g(x)={e^x}-{x^2}+\frac{{3({a+1})}}{2}x-3a≥0$恒成立.必需g(0)=1-3a≥0,a$≤\frac{1}{3}$,则$-1≤a≤\frac{1}{3}$.
g′(x)=ex-2x+$\frac{3(a+1)}{2}$=h(x).
h′(x)=ex-2,可知:x=ln2时h(x)即g′(x)取得极小值即最小值.
g′(ln2)=2-2ln2+$\frac{3(a+1)}{2}$.
由$-1≤a≤\frac{1}{3}$,∴g′(ln2)≥2-2ln2>0,
∴函数g(x)在x∈[0,+∞)上单调递增,
因此$-1≤a≤\frac{1}{3}$.
点评 本题考查了利用导数研究函数的单调性极值与最值并且研究方程的根的个数、恒成立问题的等价转化方法、分类讨论方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
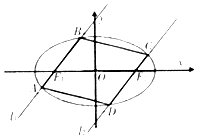 如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.
如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x,y都不为0 | B. | x≠y且x,y都不为0 | C. | x≠y且x,y不都为0 | D. | x,y不都为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com