

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
分析 (Ⅰ)由已知条件求出第二组的频率,从而补全频率分布直方图,
由此能求出n、a、p的值;
(Ⅱ)估计[40,45)岁与[45,50)年龄段的“环保族”人数比,
根据分层抽样原理,利用列举法求出对应的概率.
解答 解:(Ⅰ)第二组的频率为:
1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
∴高为$\frac{0.03}{5}$=0.06,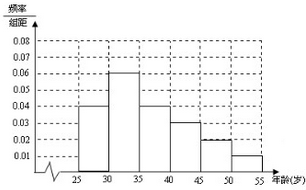
频率分布直方图如图所示;
第一组的人数为$\frac{120}{0.6}$=200,频率为0.04×5=0.2,
∴n=$\frac{200}{0.2}$=1000;
由题意知第二组的频率为0.3,
∴第二组的人数为1000×0.3=300,
∴p=$\frac{195}{300}$=0.65,
第四组的频率为0.03×5=0.15,
∴第四组的人数为1000×0.15=150,
∴a=150×0.4=60;
(Ⅱ)∵[40,45)岁年龄段的“环保族”人数
与[45,50)年龄段的“环保族”人数的比值为60:30=2:1,
∴采用分层抽样抽取6人,
其中[40,45)岁中有4人,记为a、b、c、d,
[45,50)岁中有2人,记为E、F,
从这6人中选取2人,基本事件是
ab、ac、ad、aE、aF、bc、bd、bE、bF、cd、cE、cF、dE、dF、EF共15种,
选取的2名恰有1人年龄在[40,45)的基本事件是aE、aF、bE、bF、cE、cF、dE、dF共8种,
故所求的概率为P=$\frac{8}{15}$.
点评 本题考查了频率分布直方图与古典概型的概率计算问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{3\sqrt{2}}{2π}$ | C. | $\frac{\sqrt{3}}{3π}$ | D. | $\frac{2\sqrt{3}}{3π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -71 | C. | 64 | D. | 199 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
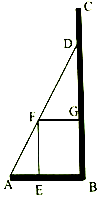 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com