练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．某厂生产甲、乙两种产品，生产甲种产品每件要消耗煤9吨，电力4千瓦，使用劳动力3个，获利70元；生产乙种产品每件要消耗煤4吨，电力5千瓦，使用劳动力10个，获利120元．有一个生产日，这个厂可动用的煤是360吨，电力是200千瓦，劳动力是300个，问应该如何安排甲、乙两种产品的生产，才能使工厂在当日的获利最大，并问该厂当日的最大获利是多少？

    分析 先设每天生产A、B产品各x、y吨，利润总额为z元，根据题意抽象出x，y满足的条件，建立约束条件，作出可根据目标函数z=70x+120y，利用截距模型，平移直线找到最优解，即可．

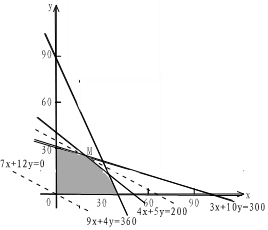    解答 解：设A、B产品各x、y吨，则由题意，$\left\{\begin{array}{l}{9x+4y≤360}\\{4x+5y≤200}\\{3x+10y≤300}\\{x，y≥0}\end{array}\right.$（3分）
    z=70x+120y（4分）
    作出以上不等式组的可行域，如图（8分）
    由图知在$\left\{\begin{array}{l}{4x+5y=200}\\{3x+10y=300}\end{array}\right.$的交点M（20，24）处取最大值 （10分）
    zmax=70×20+120×24=4280（元）
    答：A、B产品各生产20千克、24千克时获得最大效益为4280元． （12分）

    点评 本题主要考查用线性规划解决实际问题中的最值问题，基本思路是抽象约束条件，作出可行域，利用目标函数的类型，找到最优解．属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=$\frac{1}{x}$-alnx（a∈R）．
    （1）当a=-1时，求f（x）的单调递减区间；
    （2）若函数f（x）有唯一的零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若m=2x2+2x+1，n=（x+1）2，则m，n的大小关系为（　　）
    A．m＞nB．m≥nC．m＜nD．m≤n

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．（在复数范围内）解方程|z|+（z+$\overline{z}$）i=$\frac{3-i}{2+i}$，求解复数z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．甲、乙两位学生参加全国数学联赛培训．在培训期间，他们参加的5次测试成绩记录如下：
    甲：82   82   79   95   87
    乙：95   75   80   90   85
    （Ⅰ）从甲、乙两人的这5次成绩中各随机抽取一个，求甲的成绩比乙的成绩高的概率；
    （Ⅱ）现要从甲、乙两位同学中选派一人参加正式比赛，从统计学的角度考虑，你认为选派哪位同学参加合适？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=ex-ax有两个零点x1＜x2，则下列说法正确的个数是（　　）
    ①a＞e；②x1+x2＞2；③x1x2＞1；④函数f（x）有极小值点x0，x1+x2＜2x0．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．求值：$\frac{{2sin{{47}°}-\sqrt{3}sin{{17}°}}}{{cos{{17}°}}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．方程x2sinα-y2cosα=1，0＜α＜π表示焦点在y轴上的椭圆，则α的取值范围是（$\frac{π}{2}$，$\frac{3π}{4}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，（$\overrightarrow{a}-\overrightarrow{b}$）⊥$\overrightarrow{a}$
    （1）求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角及向量$\overrightarrow{b}$在向量$\overrightarrow{a}$方向上的投影；
    （2）求|2$\overrightarrow{a}-\overrightarrow{b}$|的值；
    （3）若向量$\overrightarrow{c}$=3$\overrightarrow{a}$+5$\overrightarrow{b}$，$\overrightarrow{d}$=m$\overrightarrow{a}$-3$\overrightarrow{b}$，$\overrightarrow{c}∥\overrightarrow{d}$，求m的值．

    查看答案和解析>>

    同步练习册答案