练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

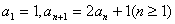
    在数列中，若，设，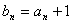

    （1）求证：数列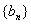 是等比数列；   （2）求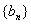，的通项公式.

     


    （1）详见解析；（2），.

    试题解析：（1）∵，∴，又∵，

    ∴，，即数列是以为首项，为公比的等比数列；

    （2）由（1）可知，，又∵，∴.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


        已知矩阵，，向量，为实数，若，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：

    非统计专业

    统计专业

    男

    13

    10

    女

    7

    20

    根据表中的数据断定主修统计专业与性别有关系，这种判断出错的可能性为____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    公差不为零的等差数列的前项和为.若是的等比中项, ,则等于 （    ）         

    A.  96        B.  108           C.  145        D.  160   

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义：我们把满足（是常数）的数列叫做等和数列，常数叫做数列的公和.若等和数列的首项为1，公和为3，则该数列前2010项的和            .  

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    掷两枚骰子，出现点数之和为的概率是（   ）

    A．         B．       C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某工厂对一批新产品的长度（单位： ）进行检测，如图5是检测结果的频率分布直方图，据此估计这批产品的中位数为（    ）

    A．       B．        C．       D．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有5名优秀毕业生到母校的3个班去作学习经验交流，则每个班至少去一名的不同分派方法种数为

    A.      B.      C.        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


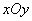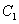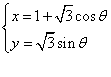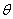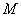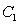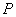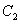    在直角坐标系中，曲线的参数方程为（其中为参数），点是曲线上的动点，点在曲线上，且满足.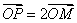

    （1）求曲线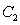的普通方程；

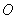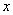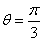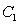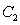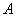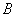    （2）以原点为极点，轴的正半轴为极轴建立极坐标系，射线与曲线、分别交于、两点，求.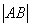

    查看答案和解析>>

    同步练习册答案