
某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
根据表中的数据断定主修统计专业与性别有关系,这种判断出错的可能性为____________.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
 已知椭圆
已知椭圆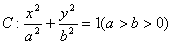 的右焦点为F,离心率为
的右焦点为F,离心率为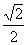 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为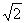 ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求椭圆C的方程
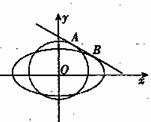
(Ⅱ)如图所示,设直线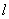 与圆
与圆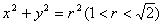 、椭圆C同时相切,切点分别为A,B,求|AB|的最大值.
、椭圆C同时相切,切点分别为A,B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
箱中装有标号为1,2,3,4,5,6且大小相同的6个球.从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖(每人一次),则恰好有3人获奖的概率是( )
A.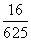 B.
B.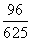 C.
C. D.
D.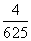
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为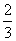 ,
,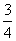 ,
,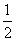 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量ξ,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com